• Ciência Dura

Como a fórmula quadrática evoluiu, da Babilônia para a aula de matemática moderna

A fórmula quadrática não é apenas algo que os professores usam para torturar os alunos de álgebra. Os babilônios uma vez o usaram para calcular impostos.

Crédito: benjaminec / Adobe Stock

Principais conclusões

• Em seu novo livro, A arte de mais: como a matemática criou a civilização, autor Michael Brooks explora a evolução da matemática e seus amplos impactos nas sociedades antigas e modernas.
• Este trecho apresenta uma visão geral da evolução da álgebra e, mais especificamente, da fórmula quadrática.
• O que começou como uma ferramenta de cobrança de impostos evoluiu para uma fórmula que os alunos ainda aprendem hoje.

Extraído de A ARTE DE MAIS: COMO A MATEMÁTICA CRIOU A CIVILIZAÇÃO por Michael Brooks. Direitos autorais 2022 de Michael Brooks. Extraído com permissão da Pantheon Books, uma divisão da Penguin Random House LLC. Todos os direitos reservados. Nenhuma parte deste trecho pode ser reproduzida ou reimpressa sem permissão por escrito do editor.

Resolvendo a equação quadrática

O que é mesmo álgebra? Você pode pensar nisso - com toda razão, dado como tradicionalmente é ensinado - como um labirinto aterrorizante de equações, uma sopa de letrinhas de x, y, z, a, b, e c , mais alguns sobrescritos (^doise³e talvez até⁴). Para os não iniciados, é certamente desanimador. Mas não há razão para a álgebra ser problemática. É realmente apenas a arte de desvendar informações ocultas usando o que sabemos.

O nome da álgebra vem da palavra al-jabr no título do livro do século IX de Muhammad al-Khwārizmī (nós o encontramos no Capítulo 1 como O livro compêndio sobre cálculo por conclusão e balanceamento ). Isso reúne ideias egípcias, babilônicas, gregas, chinesas e indianas sobre encontrar números desconhecidos, dadas algumas outras. Al-Khwārizmī nos dá prescrições — fórmulas que chamamos de algoritmos — para resolver as equações algébricas básicas, como machado^dois+ bx = c , e métodos geométricos para resolver 14 tipos diferentes de equações 'cúbicas' (onde x é elevado à potência de 3).

Nesse ponto da história, aliás, não havia x , nem nada realmente elevado a qualquer poder, nem mesmo quaisquer equações no que al Khwārizmī escreveu. A álgebra era originalmente “retórica”, usando um emaranhado de palavras para apresentar um problema e explicar a solução. O fator oculto procurado era geralmente referido como o cossa , ou 'coisa', e assim a álgebra era muitas vezes conhecida como a 'Arte Cossick': a Arte da Coisa. Um estudante precoce da Arte Cossick pode se encontrar cara a cara com algo assim:

Dois homens conduziam bois por uma estrada, e um disse ao outro: Dê-me dois bois, e terei tantos quantos você tem. Então o outro disse: Agora você me dá dois bois, e eu terei o dobro do número que você tem. Quantos bois havia e quantos cada um tinha?

ou

Eu tenho um único pano de linho que tem 60 pés de comprimento e 40 pés de largura. Desejo cortá-lo em porções menores, cada uma com 6 pés de comprimento e 4 pés de largura, de modo que cada pedaço seja grande o suficiente para fazer uma túnica. Quantas túnicas podem ser feitas com um único pano de linho?

Esses exemplos foram coletados por Alcuin de York por volta de 800 dC e publicados em um compêndio de quebra-cabeças chamado Problemas para aguçar os jovens . Eles não são tão diferentes das perguntas que enfrentamos nas aulas de matemática na escola. No entanto, tínhamos a vantagem de poder transformá-los em equações; vale a pena fazer uma pausa, antes de nos aprofundarmos na álgebra, para apreciar o quanto isso nos torna privilegiados.

Foi apenas no século 16 que alguém pensou em afastar a álgebra das palavras. A ideia veio a um funcionário público francês chamado François Viète. Depois de se formar como advogado, Viète passou a maior parte de sua vida profissional a serviço da corte real francesa, ajudando no que fosse solicitado. Ele era um administrador na Bretanha, um conselheiro privado real de Henrique III e decifrador de códigos de Henrique IV. O momento de maior orgulho de Viète pode ter ocorrido quando o rei da Espanha acusou a corte francesa de feitiçaria. De que outra forma, queixou-se ele ao papa, a França poderia ter conhecimento dos planos militares da Espanha? Mas não havia feitiçaria, é claro. Viète era simplesmente mais esperto do que os codificadores espanhóis e conseguiu descriptografar suas comunicações quando soldados franceses as interceptaram.

Talvez tenha sido essa mesma agilidade mental que permitiu a Viète ver que a álgebra retórica seria mais fácil se fosse codificada como símbolos. Em sua álgebra, ele usou consoantes para designar parâmetros e vogais para os itens desconhecidos. Ele escreveria algo como:

PARA cubo + B. quad. dentro PARA igual B. quad. dentro COM

onde agora escreveríamos

PARA³+ B^doisA = B^doisCOM

Ainda não foi fácil, se formos honestos, mas foi um começo. É interessante notar que o sinal de mais está aqui (e ele usou sinais de menos em outros lugares), mas o sinal de igual não está. O matemático galês Robert Recorde introduziu nosso sinal de igual em 1557, em seu livro intitulado A pedra de amolar da inteligência, que é a segunda parte da Aritmética: contendo a extração de Rootes: A prática Cossike, com a regra da Equação: e as obras de Surde Nombers.

E enquanto estamos no assunto de notação, vale a pena notar que a razão pela qual a letra 'x' foi associada à coisa desconhecida ainda é muito contestada. De acordo com o historiador cultural Terry Moore, é porque a álgebra original de al-Khwārizmī usava al-shay-un para significar 'a coisa indeterminada'. Quando os tradutores espanhóis medievais procuravam um equivalente latino, eles usavam a coisa mais próxima que tinham de 'sh', que na verdade não existe em espanhol. E assim acabamos com a letra que faz o som do 'ch' espanhol: x. Mas outras fontes dizem que é para René Descartes, que simplesmente colocou os dois extremos do alfabeto para trabalhar em seu livro de 1637 Geometria . Ele generalizou os parâmetros conhecidos para a, b, e c ; os desconhecidos foram designados x e y e com.

Se você se sente intimidado pela ideia de álgebra, com todas as suas notações enigmáticas, pode se beneficiar pensando nela apenas como uma forma de traduzir formas geométricas em forma escrita.

Ao estruturar este livro, fiz uma distinção artificial entre álgebra e geometria. Embora normalmente os aprendamos como tópicos distintos - principalmente porque facilita a elaboração de currículos escolares - a álgebra flui perfeitamente da geometria; é a geometria feita sem imagens, um movimento que a liberta e permite que a matemática floresça. Para ver como, voltemos – como sempre, parece – às antigas práticas de tributação.

Como vimos em nossa análise da geometria, os impostos eram frequentemente baseados em áreas de campo - a palavra babilônica para área, igual , originalmente significava 'campo'. Não é à toa que os administradores babilônicos tiveram que aprender a resolver quebra-cabeças como este oferecido no antigo tablet babilônico YBC 6967, que fica na coleção de Yale:

A área de um retângulo é 60 e seu comprimento excede sua largura em 7. Qual é a largura?

Vamos tentar resolver. Se a largura é x, o comprimento é x + 7. A área de um retângulo é simplesmente a largura multiplicada pelo comprimento, então a área A é dada por esta equação:

A = x(x + 7)

Os parênteses aqui dizem para você multiplicar cada uma das coisas dentro dos parênteses pela coisa imediatamente fora dele, o que leva a:

PARA = x^dois+ 7x

Os babilônios resolveriam isso por meio de uma série de etapas que ilustram a estreita conexão entre álgebra e geometria. O processo é conhecido como “completar o quadrado”.

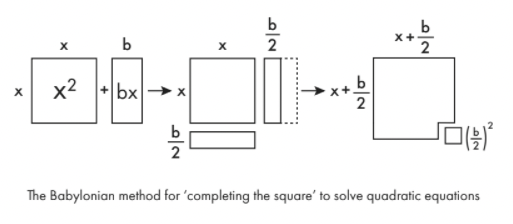
Para fazer uma equação do tipo x^dois+ bx gerenciável, você primeiro desenha como formas geométricas. x^dois é apenas um quadrado de lado x. bx é um retângulo de comprimento x e largura b. Divida esse retângulo em dois no sentido do comprimento e mova uma metade para a parte inferior do quadrado original, e você quase pode fazer um quadrado maior. Para completar esse quadrado maior, você só precisa adicionar um pequeno quadrado de lado b/2. A área deste pequeno quadrado é ( b /dois)^dois. Então você pode ver que a expressão original é realmente equivalente a ( x + b /dois)^dois– ( b /dois)^dois.

Dada uma equação da forma

x^dois+ bx = c

os babilônios substituiriam no resultado de completar o quadrado, tornando-o:

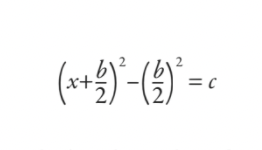
Então eles trabalhariam isso e reduziriam tudo à fórmula (embora não tenha sido escrito como uma fórmula no sentido moderno):

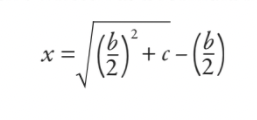
A resposta é que a largura é 5 e o comprimento é 12. Mas gostaria de saber se essa fórmula parece um pouco familiar para você? Se eu oferecer a você um ajuste na equação original para que você tenha

machado^dois+ bx + c = 0

você resolveria isso usando uma fórmula que aprendeu na escola - a fórmula quadrática:

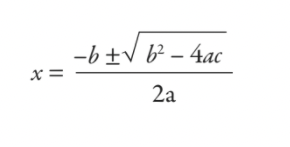
Como você pode ver claramente, o que você aprendeu na escola é pouco mais do que uma ferramenta de cálculo de impostos de 5.000 anos. No entanto, nenhum de nós cresce para ser oficial de impostos da Babilônia – então por que os alunos estão aprendendo a fórmula quadrática hoje em dia? É uma pergunta justa e que causa discussões até mesmo entre professores de matemática.

Neste artigo história da cultura matemática

Compartilhar: