• Começa Com Um Estrondo

Pergunte a Ethan: O que significa a Grande Teoria Unificada?

Se as forças eletromagnética e fraca se unem para fazer a força eletrofraca, talvez, em energias ainda mais altas, algo ainda maior aconteça?

A ideia de unificação sustenta que todas as três forças do Modelo Padrão, e talvez até a gravidade em energias mais altas, são unificadas em uma única estrutura. Essa ideia, embora continue popular e matematicamente convincente, não tem nenhuma evidência direta que apoie sua relevância para a realidade. (Crédito: ABCC Austrália, 2015)

Principais conclusões

• No Modelo Padrão da física de partículas, excluindo a gravidade, existem três forças quânticas fundamentais: o eletromagnetismo, mais as forças nucleares fortes e fracas.
• Em altas energias, as forças eletromagnética e fraca se unem, criando a força 'eletrofraca'. Isso significa que, em energias ainda mais altas, todas as forças se unem?
• Esta ideia, da Grande Unificação, tem sido interessante e convincente por quase 50 anos. Veja como pensar sobre isso, mesmo que você não saiba a matemática.

Sempre que pensamos sobre o Universo em um nível fundamental, sempre há a tentação de nos perguntar se a realidade pode de alguma forma ser mais simples do que percebemos. Por mais complexo e diversificado que seja o mundo natural, é humilhante reconhecer que tudo o que vemos, percebemos e interagimos é feito dos mesmos blocos de construção. A matéria é feita de átomos, que são feitos de prótons, nêutrons e elétrons; prótons e nêutrons são feitos de quarks e glúons. Existem outras partículas também: fótons, neutrinos e alguns primos mais pesados ​​dos quarks leves e dos elétrons. Tomado em conjunto, tudo o que não pode ser mais dividido – o que chamamos de fundamental ou elementar – compõe o moderno Modelo Padrão de partículas elementares.

E, no entanto, é natural se perguntar se as partículas e forças que conhecemos hoje não poderiam ser mais simplificadas, talvez todas emergindo de algum estado mais unificado que existiu no início da história do Universo? Essa é a questão Apoiador do Patreon Igor Zhbanov, que escreve para perguntar:

O que [significa] a Grande Teoria Unificada significa na prática? Ou seja, o que significa que no nível de energia mais alto teremos apenas um tipo de força? Por exemplo, teremos duas bolas de energia que gravitarão e se atrairão eletricamente com o mesmo valor de força simultaneamente? E teremos apenas uma fórmula para expressar todas as leis físicas? Ou como as partículas se comportarão sob essa força unificada?

Apesar do fato de nomes como Grand Unified Theory ou Grand Unification parecerem simples, é uma das ideias mais difíceis da física teórica para realmente entender. Vamos explorar do que se trata.

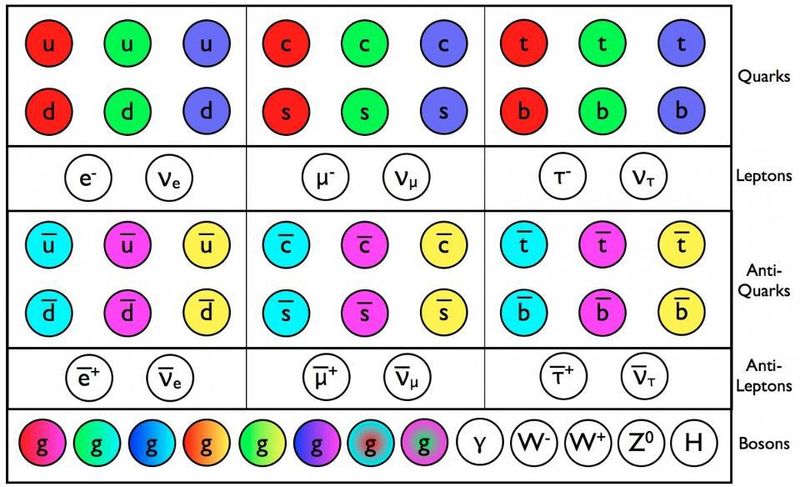
Os quarks, antiquarks e glúons do modelo padrão possuem uma carga de cor, além de todas as outras propriedades como massa e carga elétrica. Todas essas partículas, até onde podemos dizer, são realmente pontuais e vêm em três gerações. Em energias mais altas, é possível que ainda existam tipos adicionais de partículas. ( Crédito : E. Siegel/Além da Galáxia)

Esta imagem, acima, mostra o Modelo Padrão de partículas elementares que existe há mais de 50 anos. Em 2011, o bóson de Higgs – a partícula final que ainda não havia sido detectada – revelou-se no Grande Colisor de Hádrons no CERN: o culminar de quase meio século de busca por ele. Com sua descoberta, finalmente conseguimos completar o Modelo Padrão, que descreve todas as partículas conhecidas existentes. (Nota: o Modelo Padrão não inclui matéria escura ou energia escura; estes ainda são mistérios.)

De acordo com o Modelo Padrão, existem três forças fundamentais que ele descreve.

1. O força eletromagnética , que atua sobre partículas que possuem uma carga elétrica fundamental (positiva ou negativa) e que podem ser atrativas ou repulsivas. O fóton é a única partícula que medeia a força eletromagnética.
2. O força nuclear fraca , que atua em partículas que possuem uma propriedade (muito menos conhecida) chamada isospin fraco ou carga fraca . Embora possa ser atrativa ou repulsiva, a força fraca é muito mais conhecida por seu envolvimento em decaimentos radioativos, em fissão e fusão nuclear e por alterar o sabor (ou seja, o tipo) de quarks e léptons. Existem três partículas, a dois bósons W carregados e o bóson Z neutro , que medeiam a força fraca.
3. E a força nuclear forte , que atua apenas em partículas que possuem carga de cor : os quarks e os outros glúons, exclusivamente. A força forte tem a estranha propriedade de exercer uma força insignificantemente pequena em distâncias muito pequenas, mas de fazer a força crescer muito quando a distância entre as partículas aumenta: uma propriedade chamada liberdade assintótica. Ele mantém prótons e nêutrons (e todas as partículas feitas de quarks e/ou antiquarks) unidos, e há oito glúons que o mediam.

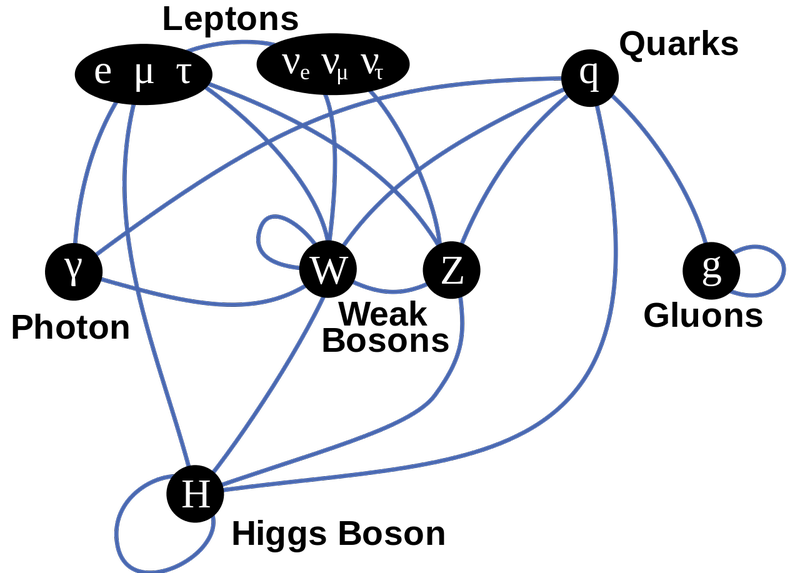
Este diagrama das partículas do Modelo Padrão mostra os férmions na linha superior, os bósons de calibre na linha do meio e os Higgs na parte inferior. As linhas indicam acoplamentos, e você pode ver quais partículas fermiônicas se acoplam a quais forças pelas linhas azuis. Tudo com casais em massa para o Higgs; as únicas partículas que não têm massa (e, portanto, não têm) são o fóton e os glúons. ( Crédito : TriTertButoxy/Stannered na Wikipedia em inglês)

No entanto, essas três forças não são completamente independentes uma da outra. Algumas partículas, como os quarks, podem experimentar todas essas três interações. Outras partículas, como o elétron, o múon e o tau, só podem experimentar as forças eletromagnética e nuclear fraca. Outros ainda, como os neutrinos, só podem experimentar a força fraca, enquanto o fóton só pode experimentar a força eletromagnética. Essa sobreposição é o motivo pelo qual não temos simplesmente três teorias separadas para as três forças fundamentais, mas sim uma teoria abrangente – o Modelo Padrão – que explica como todas elas funcionam em conjunto.

Uma das descobertas importantes que ocorreram no início da década de 1960 foi a percepção de que a força eletromagnética e a força fraca não poderiam ser descritas como completamente independentes uma da outra, mas sim que há uma interação entre as duas. Você não pode apenas explicar a força fraca com isospin fraco e a força eletromagnética com carga elétrica, mas precisa haver um novo número quântico que une os dois: hipercarga fraca , que foi introduzido pela primeira vez por Shelly Glashow em 1961 .

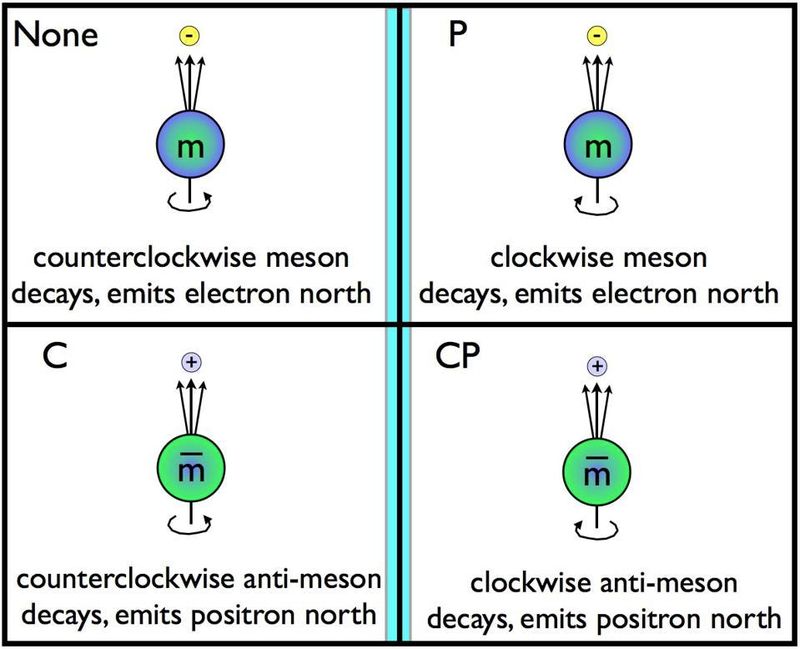
A paridade, ou simetria-espelho, é uma das três simetrias fundamentais no Universo, juntamente com a simetria de reversão de tempo e conjugação de carga. Se as partículas giram em uma direção e decaem ao longo de um eixo específico, lançá-las no espelho deve significar que elas podem girar na direção oposta e decair ao longo do mesmo eixo. Observou-se que este não é o caso dos decaimentos fracos, que são as únicas interações conhecidas por violar a simetria de conjugação de carga (C), a simetria de paridade (P) e a combinação (CP) dessas duas simetrias também. ( Crédito : E. Siegel/Além da Galáxia)

Quando os físicos de partículas falam sobre o Modelo Padrão, normalmente o fazem no contexto da teoria dos grupos. Você deve ter notado que o Modelo Padrão contém:

• 1 bóson mediando as interações eletromagnéticas,
• 3 bósons mediando as interações fracas,
• e 8 bósons mediando as interações fortes,

e você deve ter notado o que poderia ser a sugestão de um padrão lá. O número 3 passa a ser 2^dois– 1, e o número 8 passa a ser 3^dois– 1. Isso não é coincidência e pode ser explicado no contexto da teoria dos grupos.

Duas das propriedades mais comuns dos grupos são ortogonalidade , OU , que é uma propriedade matemática que corresponde à operação de como os objetos giram, e unidade , você , que é uma propriedade matemática que corresponde à operação de multiplicação de matrizes. Se você perguntar, quantos elementos você precisa para descrever um grupo unitário? a resposta depende do tamanho da matriz. Se a matriz for uma matriz 1 × 1, você (1), você precisa de 1 elemento. Se for 2 × 2, você (2), você precisa de 4 elementos. Se for 3 × 3, você (3), você precisa de 9 elementos.

E se a matriz tem uma propriedade especial – que seu determinante matemático é 1 – essa é uma restrição adicional: isso retira um dos elementos. Então, se sua matriz 2 × 2 não é apenas um grupo unitário, mas é um grupo unitário especial, SEU (2), você só precisa de 3 elementos, não de 4. E se sua matriz 3 × 3 não for apenas um grupo unitário, mas um grupo unitário especial, SEU (3), você só precisa de 8 elementos, não de 9.

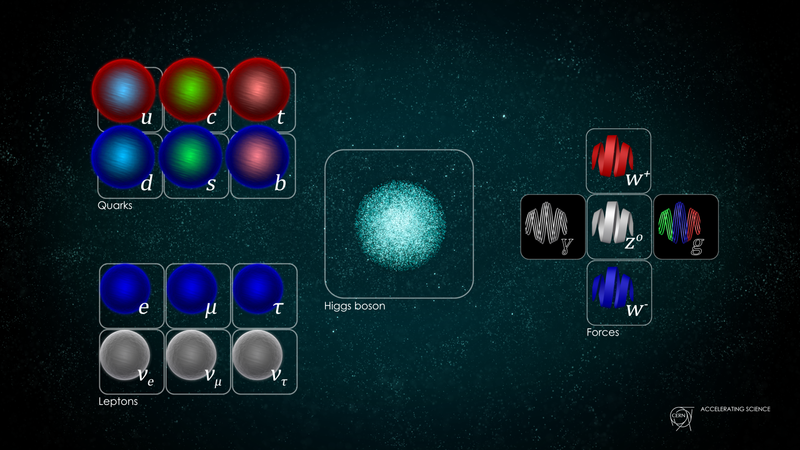
À direita, estão ilustrados os bósons de calibre, que medeiam as três forças quânticas fundamentais do nosso Universo. Há apenas um fóton para mediar a força eletromagnética, existem três bósons mediando a força fraca e oito mediando a força forte. Isso sugere que o Modelo Padrão é uma combinação de três grupos: U(1), SU(2) e SU(3). ( Crédito : Daniel Domingues/CERN)

Apenas a partir disso, você pode antecipar que, muito possivelmente, o Modelo Padrão teria a estrutura de ser uma matriz unitária especial 3 × 3 para as interações fortes, uma matriz unitária especial 2 × 2 para as interações fracas e uma matriz unitária 1 × 1 matriz unitária para as interações eletromagnéticas.

Nós escreveríamos isso como SEU (3) ⊗ SEU (2) ⊗ você (1), e identificar o SEU (3) parte com as interações fortes, o SEU (2) parte com as interações fracas, e o você (1) parte com as interações eletromagnéticas.

Isso está perto! O problema com essa interpretação é que sabemos que os componentes eletromagnéticos e fracos do Modelo Padrão se sobrepõem e não podem ser separados de forma clara. (Este era o ponto de precisar de hipercarga fraca, como Glashow mostrou!) você (1) parte não pode ser puramente eletromagnética, e a SEU (2) parte não pode ser puramente fraca; tem que haver mixagem aí. É por isso que dizemos que é a força eletrofraca e que esses dois grupos precisam trabalhar juntos: SEU (2) ⊗ você (1), para descrever a interação eletrofraca. Se descrevermos as coisas dessa maneira, obteremos o Modelo Padrão como o conhecemos, e a matemática nos permite atribuir partículas com base nas propriedades que se prevê que tenham.

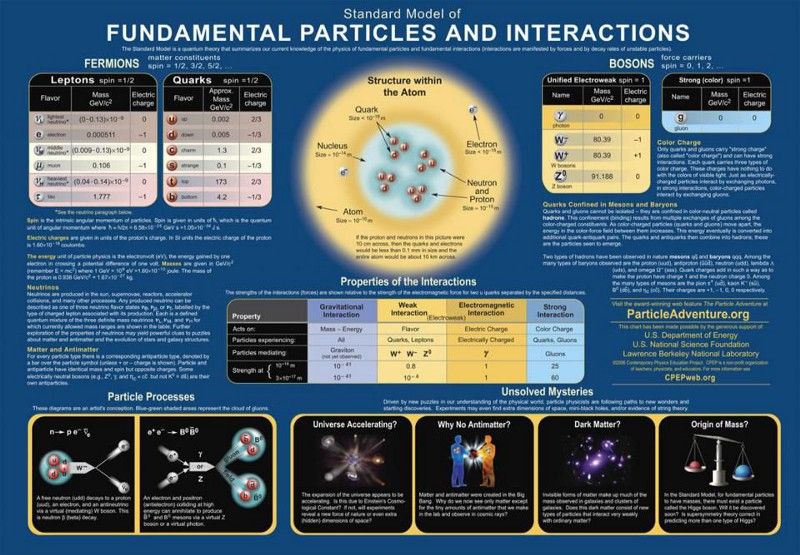
As partículas e forças do Modelo Padrão. Qualquer teoria que afirme ir além do Modelo Padrão deve reproduzir seus sucessos sem fazer previsões adicionais que já demonstraram não ser verdadeiras. O comportamento patológico que já seria descartado é a maior fonte de restrições em cenários fora do Modelo Padrão, incluindo grandes teorias unificadas. ( Crédito : Projeto de Educação Física Contemporânea/DOE/SNF/LBNL)

O fato de que cada partícula que foi prevista existe e foi verificada como tendo as propriedades que elas têm é um tremendo sucesso para o Modelo Padrão, e por que todas as alternativas caíram no esquecimento.

Mas é natural se perguntar sobre algumas questões, começando com: o Modelo Padrão é tudo o que existe, ou pode haver alguma simetria subjacente maior que se tornaria aparente em energias muito mais altas? Existem novas partículas e novas interações e, portanto, novos fenômenos físicos que ainda precisam ser detectados por aí? E em caso afirmativo, que tipo de estrutura, inclusive no contexto da teoria dos grupos, ela possui?

É daí que vem a ideia de uma grande teoria unificada, conhecida como GUT ou como grande unificação no conceito. O ponto de partida é o Modelo Padrão, que em formato de teoria de grupos é SEU (3) ⊗ SEU (2) ⊗ você (1). Ele então nos ensina a procurar um grupo maior que contém o Modelo Padrão, mas que incorpora o Modelo Padrão em alguma estrutura maior com um grau mais alto de simetria. Essa estrutura, necessariamente, também inclui partículas adicionais e/ou acoplamentos adicionais, e também traz consigo novas previsões, pois serão permitidos processos que são suprimidos ou totalmente proibidos no Modelo Padrão, e, portanto, obrigatório , nestas grandes teorias unificadas.

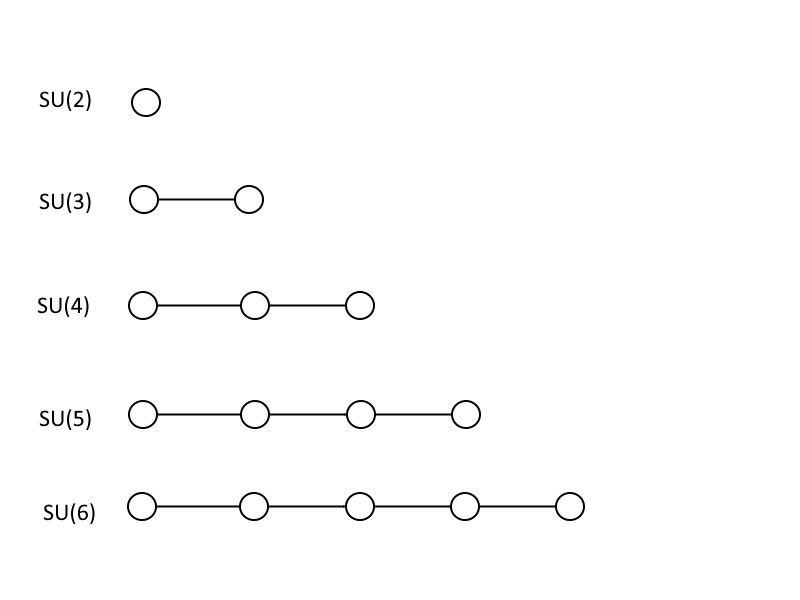
Estes são os diagramas de Dynkin que representam os primeiros 5 grupos unitários especiais: SU(2), SU(3), SU(4), SU(5) e SU(6). Observe que cada grupo maior contém todos os que são menores do que ele e que você pode continuar para grupos cada vez maiores sem limites seguindo esse padrão. (Crédito: E. Siegel)

Para mostrar como funcionam as grandes teorias unificadas, vou ensinar um pouco de matemática, embora, a menos que você seja um matemático ou um físico, talvez nem reconheça isso como matemática. As imagens acima, que parecem círculos conectados por linhas, são conhecidas como Diagramas de Dynkin . Se você tem um círculo por si só, isso corresponde a SEU (2), que é uma matriz 2 × 2 com determinante de 1. Se você tiver dois círculos conectados um ao outro, isso é SEU (3): uma matriz 3 × 3 com um determinante de 1. Você pode continuar adicionando círculos e conectando-os da mesma forma, onde o número de círculos conectados mais um informa o tamanho de sua matriz e, portanto, o tamanho de seu grupo unitário especial. O Modelo Padrão contém um SEU (3), um SEU (2), e um você (1), onde o último não recebe um símbolo no mundo dos diagramas de Dynkin.

Outro tipo de grupo que aparece muito na grande unificação é o ortogonal especial, ASSIM , conjunto de grupos. Em vez de círculos apenas conectados por uma única linha em uma cadeia, o diagrama de Dynkin para os grupos ortogonais especiais (de número par) tem uma estrutura ramificada, onde o penúltimo círculo não se conecta apenas ao último no final, mas tem um círculo extra saindo dele.

ASSIM (6), como você pode ver abaixo, tem o mesmo diagrama de Dynkin estruturado como SEU (4), mas todos os outros diagramas são exclusivamente diferentes, onde o número dentro dos parênteses é sempre o dobro do número de círculos. Depois de obter o padrão, é muito fácil ver que você pode construir tanto o seu SEU (n+1) e seu ASSIM (2n) grupos do tamanho que você quiser, sem limite.

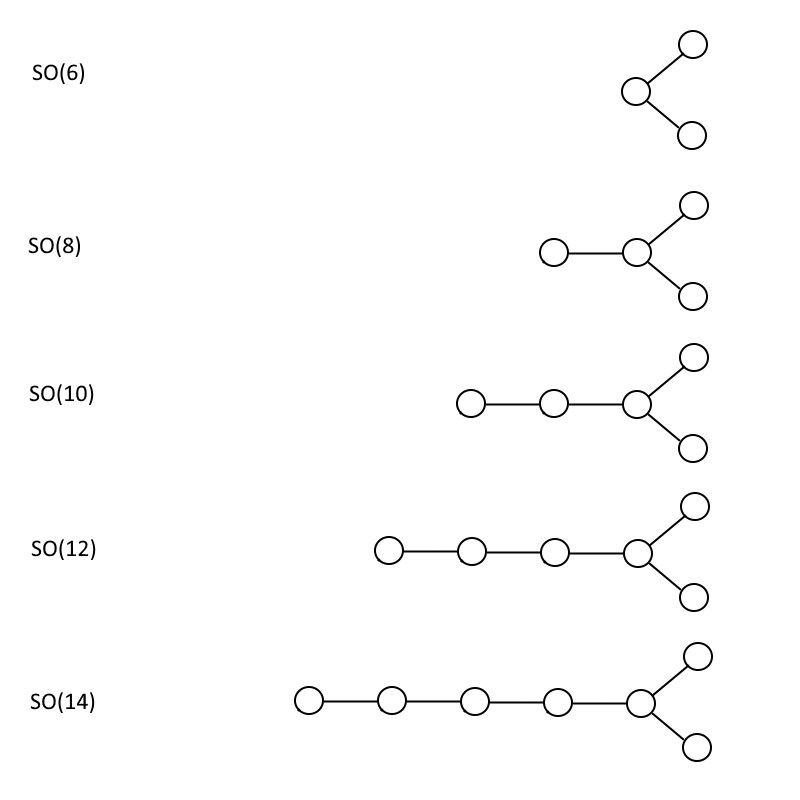
Os grupos ortogonais especiais de número par, mostrados para SO(6), SO(8), SO(10), SO(12) e SO(14). Esse padrão pode ser continuado indefinidamente, e o grupo SO(32) contém algumas propriedades matemáticas que o tornam muito atraente do ponto de vista teórico das cordas. (Crédito: E. Siegel)

Mas não precisamos ficar arbitrariamente grandes; só precisamos ser grandes o suficiente para que possamos incorporar todo o Modelo Padrão em nosso grupo.

Como descobrimos isso?

Aqui está uma regra muito útil quando se trata da matemática dos diagramas de Dynkin: toda vez que você apaga um círculo do seu diagrama, você também apaga as linhas que o conectam aos outros círculos, e cada apagamento também pode lhe dar um bônus você (1) grupo que vem de graça.

Então, se quiséssemos incorporar o Modelo Padrão, que é SEU (3) ⊗ SEU (2) ⊗ você (1), em um grupo maior, qual é o grupo de tamanho mínimo que precisaríamos para fazer isso?

No lado unitário especial, SEU (5) o fará. Se você tiver quatro círculos conectados por (três) linhas, tudo o que você precisa fazer é apagar um dos dois círculos do meio. Onde você fica com dois círculos conectados por uma linha, isso é SEU (3). Onde você tem um único círculo deixado isolado por si mesmo, isso é SEU (2). E você também ganha um grátis você (1) fora do ato de apagar, então aí está, seu Modelo Padrão: SEU (3) ⊗ SEU (2) ⊗ você (1).

Já no lado especial ortogonal, o menor grupo que irá conter o Modelo Padrão é um pouco maior: ASSIM (10). Como você pode ver, ASSIM (10) pode conter não apenas o Modelo Padrão, mas também SEU (5) dentro dele. Neste caso, você tem que apagar dois círculos para recuperar o Modelo Padrão, e você pode escolher em qual ordem você os apaga. você (1) grupo para encerrar com o Modelo Padrão e apagar dois círculos em vez de um; ASSIM (10) é um grupo maior do que SEU (5) é, e SEU (5) é maior que o Modelo Padrão.

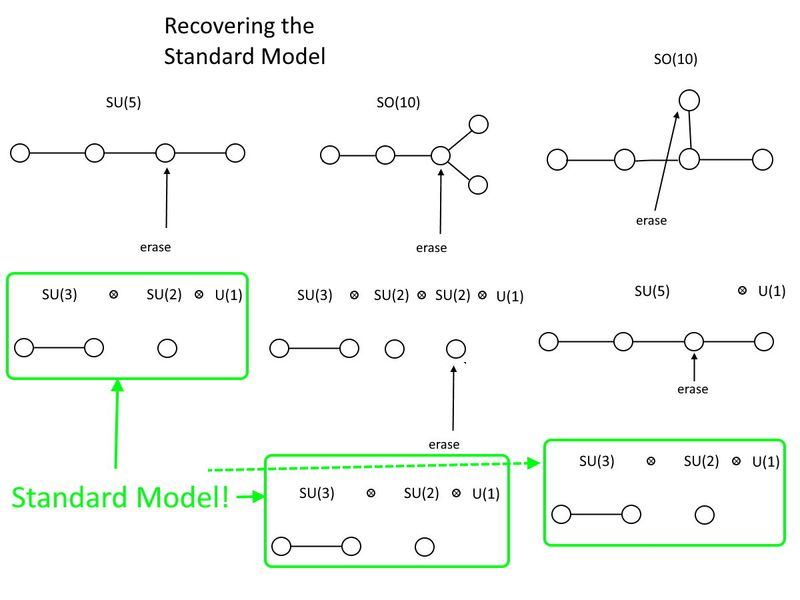
A estrutura de grupo do Modelo Padrão, SU(3) x SU(2) x U(1), pode ser incorporada em vários grupos maiores, incluindo SU(5) e SO(10). Em termos de diagramas de Dynkin, você deve apagar um ponto para obter o Modelo Padrão de SU(5) e dois pontos, em qualquer ordem que preferir, para recuperá-lo de SO(10). SO(10) também contém SU(5), e ambos contêm numerosas partículas para as quais não há evidências em nossos experimentos de física de partículas. (Crédito: E. Siegel)

Um grupo maior que contém um grupo menor (ou conjunto de grupos menores) sempre conterá todas as partículas que estão presentes no grupo menor, mais as adicionais. No Modelo Padrão, um dos aspectos mais intrigantes da realidade com que nos deparamos é que o universo não é simétrico de várias maneiras. Em particular:

• os férmions são quirais, o que significa que há diferenças entre quarks e léptons destros e canhotos,
• existem apenas neutrinos canhotos e antineutrinos destros; nunca neutrinos destros ou antineutrinos canhotos,
• e que a interação fraca, particularmente através dos bósons W, apenas se acopla aos férmions quirais esquerdos, não aos quirais direitos.

O ASSIM (10) grupo , porém, é esquerda-direita simétrica , que você pode ver explicitamente se quebrar a simetria na coluna do meio, conforme mostrado acima. No Modelo Padrão, às vezes escrevemos SEU (2) com um L como um subscrito anexado a ele, para nos lembrar que vivemos em um Universo quiral. Se, no entanto, quebrarmos ASSIM (10) apagando o círculo com três conexões, recuperamos não apenas o Modelo Padrão, mas um modelo simétrico esquerda-direita: SEU (3) ⊗ SEU (2) ⊗ SEU (2) ⊗ você (1), onde um SEU (2) teria um L e o outro teria um R ligado a ele.

Mais a SEU (5) lado , no entanto, você acaba com uma matriz 5 × 5 com 24 elementos únicos, em vez de SEU (3) ⊗ SEU (2) ⊗ você (1), que tem muito menos. Como resultado, você acaba prevendo partículas extras, conhecidas como bósons X ou Bósons X e Y , dependendo da terminologia e interações extras permitidas que eles mediam. Em particular, eles permitem acoplamentos extras entre quarks e léptons e – em total desacordo com as observações – eles preveem que o próprio próton seria fundamentalmente instável.

O conteúdo de partículas do grupo unificado grande hipotético SU(5), que contém a totalidade do Modelo Padrão mais partículas adicionais. Em particular, há uma série de bósons (necessariamente superpesados), rotulados como X neste diagrama, que contêm propriedades de quarks e léptons, juntos, e fariam com que o próton fosse fundamentalmente instável. ( Crédito : Cjean42/Wikimedia Commons; anotações de E. Siegel)

Qualquer coisa encontrada em um grupo menor que possa ser incorporada a um maior sempre existirá no maior, então todas as grandes teorias unificadas que contêm SEU (5) ou ASSIM (10) ou qualquer coisa maior também conterá esses bósons X (ou X-e-Y) e preverá o decaimento de prótons. Quanto melhor restringirmos o tempo de vida do próton, melhor poderemos restringir esses modelos. SEU (5) foi originalmente interessante porque previu o decaimento de prótons com uma vida útil de ~10³⁰anos; restrições modernas nos dizem que o tempo de vida do próton é maior do que cerca de 10^{3. 4}anos hoje, governando simples SEU (5) unificação fora. Se conseguirmos esse número até cerca de 10³⁶a 10³⁷, podemos descartar ASSIM (10) também.

No entanto, uma das razões pelas quais a grande unificação permaneceu tão convincente para os teóricos é sua conexão com a teoria das cordas . Na teoria das cordas, as partículas podem ser vistas como excitações que se movem no sentido anti-horário (para a esquerda) ou no sentido horário (para a direita), onde uma corresponde a uma corda bosônica movendo-se em 26 dimensões e a outra corresponde a uma supercorda movendo-se em 10 dimensões. Você precisa de um espaço matemático com exatamente 16 dimensões para explicar a incompatibilidade, e os dois grupos conhecidos com as propriedades certas para salvar o dia são ASSIM (32), que é enorme, e E (8) ⊗ E (8),* que é igualmente enorme. Embora não tenhamos falado sobre o (excepcional) E grupos, eu queria mostrá-los, abaixo, e observar que existem apenas três deles: E (6), E (7), e E (8). (Há também dois outros grupos excepcionais, F (4) e G (2), mas eles têm estruturas diferentes.)

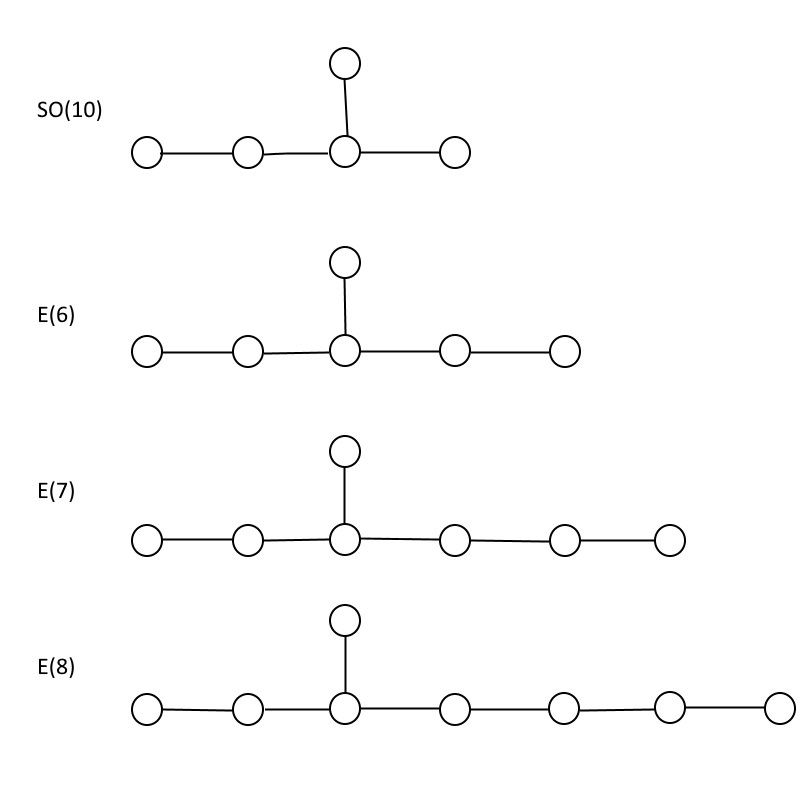
Os grupos excepcionais E(6), E(7) e E(8), em comparação com o grupo SO(10) que está embutido em todos eles. Como você pode ver, E(8) contém E(7) e E(7) contém E(6), o que significa que quaisquer partículas contidas no grupo menor também estão contidas no grupo maior, além de mais. (Crédito: E. Siegel)

Você pode se perguntar se pode ramificar do penúltimo círculo em um SEU grupo para criar um ASSIM grupo, e se você pode estender uma das ramificações curtas em um ASSIM grupo para criar um E grupo, por que você não poderia criar ramificações adicionais ou estender mais ramificações em quantidades maiores?

Bem, existe uma regra matemática simples que impede você de fazer isso e ainda atender aos requisitos de um grupo.

Se você começar em qualquer círculo onde mais de duas linhas saiam dele, há um relacionamento que você deve obedecer para ser um grupo. Em cada direção, você terá um certo número de círculos conectados por linhas: chame-os de A, B e C, onde A sempre será aquele com o menor número de círculos. A regra é esta: somente se 1/A for menor que 1/B + 1/C você é um grupo. Se 1/A for maior ou igual a 1/B + 1/C, você não é mais um grupo. Como você pode verificar rapidamente, apenas E (6), E (7), e E (8) atender a esses requisitos, com E (8) sendo o maior grupo excepcional permitido.

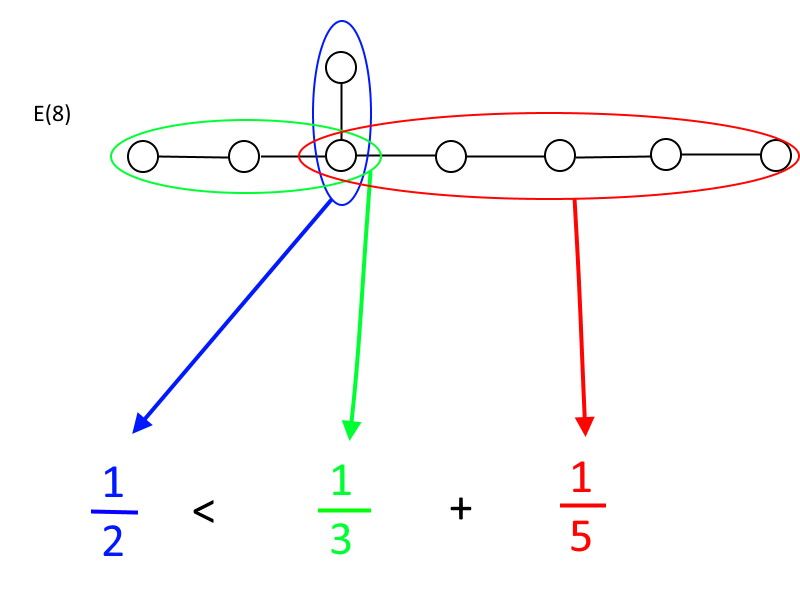
O grupo excepcional E(8) é o maior grupo excepcional permitido que ainda atende à definição matemática de grupo. Como você pode ver, estender ainda mais os segmentos verde ou vermelho das conexões círculo-e-linha faria com que a desigualdade não fosse satisfeita, tornando E(8) o maior exemplo desse tipo que permanece um grupo. (Crédito: E. Siegel)

A conclusão de tudo isso é que o Universo, se a grande unificação é uma coisa real, na verdade é mais complicado, com mais partículas e interações, do que o Modelo Padrão atualmente dita. Uma das coisas que absolutamente devem ocorrer se nosso Universo for descrito por uma grande teoria unificada é que o próton não deve ser estável, mas sim decair com algum tempo de vida finito. Outra previsão bizarra é que deve haver novas partículas hipotéticas que tenham propriedades de quarks e léptons ao mesmo tempo: leptoquarks .

Em 1997, o acelerador HERA Na Alemanha produziu um excesso de eventos que parecia ser consistente com a presença de leptoquarks, desencadeando um interesse ressurgente em grandes teorias unificadas. No entanto, dados adicionais, incluindo no Tevatron do Fermilab e mais tarde, no Large Hadron Collider, descartaram essa possibilidade em todas as energias alcançáveis ​​pelo HERA. Tal como está hoje, a ideia da grande unificação permanece teoricamente convincente, mas a evidência para isso é inexistente. Afinal, a chave para a ciência é sempre esta: se ela discorda do experimento, está errada. Não descartamos a possibilidade de que haja algum tipo de unificação que ocorra em energias extremamente altas, ainda a serem acessadas, mas com cada resultado nulo, mais rígidas se tornam as restrições às GUTs.

* – Normalmente, grupos excepcionais são escritos com o número como subscrito e não entre parênteses. Este artigo os escreveu entre parênteses para simplificar a notação para aqueles que são novos na teoria dos grupos e nos diagramas de Dynkin.

Envie suas perguntas Ask Ethan para beginwithabang no gmail ponto com !

Neste artigo, física de partículas

Compartilhar: