• Começa Com Um Estrondo

Pergunte a Ethan: O que significa que a gravidade quântica não tem simetria?

Um diagrama usado para provar que a gravidade quântica não pode ter nenhuma simetria global. A simetria, se existisse, poderia atuar apenas nas regiões sombreadas no diagrama e não causaria nenhuma alteração ao redor do ponto preto no meio. As regiões sombreadas podem ser feitas tão pequenas quanto quisermos, dividindo o círculo limite cada vez mais. Assim, a suposta simetria não atuaria em nenhum lugar dentro do círculo. (DANIEL HARLOW E HIROSI OOGURI, PRL, 122, 191601 (2019))

A busca por uma teoria quântica da gravidade é o santo graal da física. Eis por que é mais obscuro do que qualquer um esperava.

Se você quiser descrever completamente como o Universo funciona em um nível fundamental, você deve olhar para ele de duas maneiras diferentes – e incompatíveis. Para descrever as partículas e suas interações eletromagnéticas e nucleares, você precisa usar a estrutura da teoria quântica de campos (QFT), onde os campos quânticos permeiam o Universo e suas excitações dão origem às partículas que conhecemos. Para descrever como cada quantum de matéria e energia se move através do Universo, precisamos da estrutura da Relatividade Geral (GR), onde matéria e energia definem como o espaço-tempo é curvo, e o espaço-tempo curvo diz à matéria e à energia como se mover.

No entanto, essas duas teorias são mutuamente incompatíveis; para fazê-los funcionar juntos, precisaríamos desenvolver uma teoria funcional da gravidade quântica. Ainda um novo papel , recém publicado, deixou Alex Knapp intrigado, levando-o a perguntar:

O que significa isso gravidade quântica não tem simetria ?

É uma descoberta fascinante com grandes implicações. Vamos descobrir o que significa.

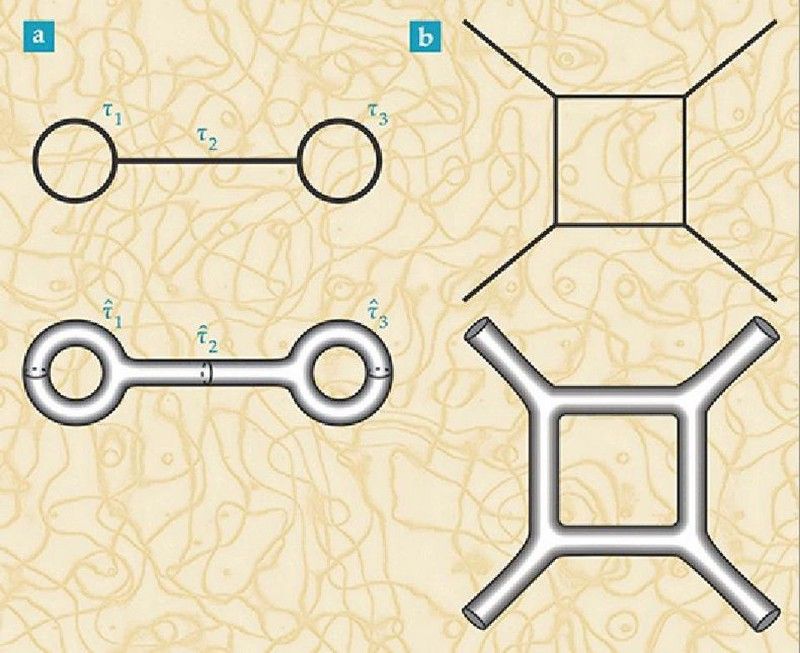
Os diagramas de Feynman (topo) são baseados em partículas pontuais e suas interações. Convertê-los em seus análogos da teoria das cordas (abaixo) dá origem a superfícies que podem ter curvatura não trivial. Na teoria das cordas, todas as partículas são simplesmente diferentes modos de vibração de uma estrutura subjacente mais fundamental: as cordas. Mas uma teoria quântica da gravidade, que a teoria das cordas aspira a ser, tem simetrias e, por associação, leis de conservação? (FIS. HOJE 68, 11, 38 (2015))

Quando você ouve a palavra simetria, provavelmente há todos os tipos de imagens que surgem em sua mente. Algumas letras do alfabeto - como A ou T - exibem uma simetria em que, se você desenhar uma linha vertical em seus centros, os lados esquerdo e direito são simétricos. Outras letras - como B ou E - têm uma simetria semelhante, mas em uma direção diferente: horizontalmente, onde as partes superior e inferior são simétricas. Ainda outros - como O - têm simetria rotacional, onde não importa quantos graus você gire, sua aparência permanece inalterada.

Estes são alguns exemplos de simetria que são fáceis de visualizar, mas não são exaustivos. Claro, alguns sistemas não têm diferenças de seus reflexos no espelho, conhecidos como simetria de paridade. Outros demonstram simetrias rotacionais, onde não importa de que ângulo você o vê. Mas há muitos outros, todos de vital importância.

Existem muitas letras do alfabeto que apresentam simetrias particulares. Observe que as letras maiúsculas mostradas aqui têm uma e apenas uma linha de simetria; letras como I ou O têm mais de um. ( MATH-ONLY-MATH.COM )

Alguns sistemas são os mesmos para a matéria e para a antimatéria: eles exibem simetria de conjugação de carga. Alguns sistemas obedecem às mesmas leis se você os evoluir para frente no tempo e se você os evoluir para trás no tempo: simetria de reversão no tempo. Outros ainda não dependem de sua localização física (simetria translacional) ou de quando você está visualizando seu sistema (simetria translacional no tempo) ou em qual quadro de referência não acelerado você ocupa (simetria de Lorentz).

Alguns sistemas físicos têm essas simetrias; outros não. Deixar cair uma bola de um penhasco obedece à simetria de reversão do tempo; cozinhar ovos mexidos não. Voar pelo espaço com os motores desligados obedece à simetria de Lorentz; acelerando, com seus motores funcionando em potência máxima, não.

O conceito de vela a laser DEEP baseia-se em uma grande matriz de laser atingindo e acelerando uma espaçonave de área relativamente grande e baixa massa. Isso tem o potencial de acelerar objetos não vivos a velocidades que se aproximam da velocidade da luz, tornando possível uma jornada interestelar dentro de uma única vida humana. O trabalho realizado pelo laser, aplicando uma força quando um objeto se move a uma certa distância, é um exemplo de transferência de energia de uma forma para outra. Um referencial acelerado é um exemplo de sistema não inercial; para esses sistemas, a simetria de Lorentz não é estritamente válida. (GRUPO DE COSMOLOGIA EXPERIMENTAL UCSB 2016)

Não são apenas os sistemas físicos que podem obedecer (ou desobedecer) simetrias. Sempre que você tiver uma equação (ou uma teoria quantitativa em geral), poderá testá-la para ver quais simetrias obedecem e quais não.

Dentro de vários QFTs, por exemplo, as partículas que experimentam a força eletromagnética obedecem a paridade, conjugação de carga e simetria de reversão no tempo, todas independentemente umas das outras. O eletromagnetismo é o mesmo para as partículas, independentemente de sua direção de movimento; o mesmo para partículas e antipartículas; o mesmo para frente no tempo e para trás no tempo.

As partículas que experimentam a força nuclear fraca, por outro lado, violam a paridade, a conjugação de carga e a reversão no tempo individualmente. Os múons canhotos decaem de forma diferente dos múons destros. Kaons neutros e anti-kaons neutros têm propriedades diferentes. E os decaimentos dos mésons B têm taxas de transformação assimétricas no tempo . Mas mesmo as interações fracas obedecem à combinação de todas as três simetrias: se você fizer um experimento com uma partícula em movimento que se move para frente no tempo e uma antipartícula com seu movimento refletido se movendo para trás no tempo, você obtém os mesmos resultados físicos.

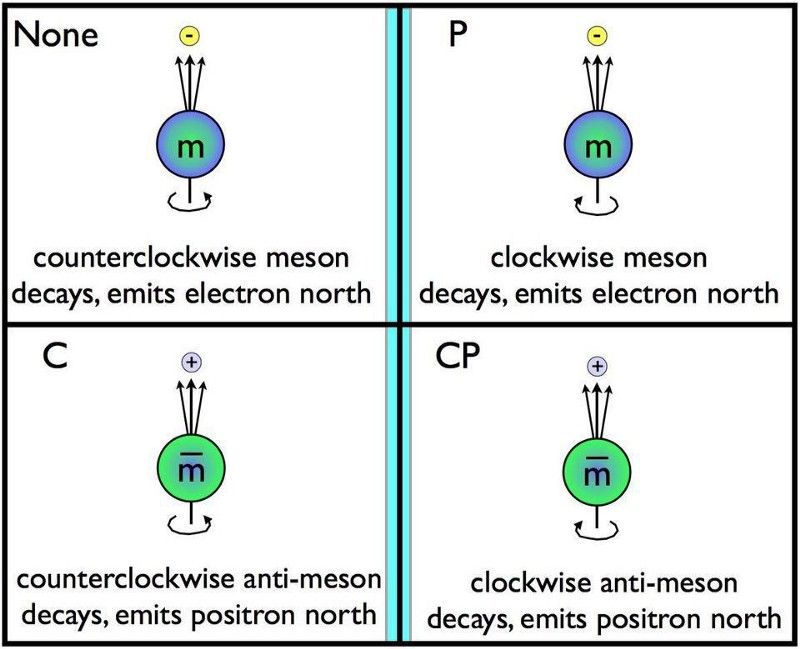
Trocar partículas por antipartículas e refleti-las em um espelho simultaneamente representa a simetria CP. Se os decaimentos anti-espelho forem diferentes dos decaimentos normais, CP é violado. A simetria de reversão de tempo, conhecida como T, é violada se CP for violado. As simetrias combinadas de C, P e T, todas juntas, devem ser conservadas sob nossas atuais leis da física, com implicações para os tipos de interações que são e não permitidas. (E. SIEGEL / ALÉM DA GALÁXIA)

Dentro de GR, vários espaços-tempos obedecem a diferentes conjuntos de simetria. O espaço-tempo (Schwarzschild) descrevendo um buraco negro não rotativo exibe simetrias de tradução de tempo, espelho e rotacional completa. O espaço-tempo (Kerr) que descreve um buraco negro em rotação exibe simetria de tradução de tempo, mas só tem simetrias rotacionais em torno de um eixo.

O espaço-tempo (Friedmann-Lemaitre-Robertson-Walker) que descreve o Universo em expansão, por outro lado, tem uma série de simetrias que obedece, mas a tradução do tempo não é uma delas: um Universo em expansão é diferente de um momento em tempo para o próximo.

Se você tivesse um espaço-tempo estático que não mudasse, a conservação de energia seria garantida. Mas se o tecido do espaço muda à medida que os objetos nos quais você está interessado se movem por eles, não há mais uma lei de conservação de energia sob as leis da Relatividade Geral. (DAVID CAMPEÃO, INSTITUTO MAX PLANCK DE RÁDIO ASTRONOMIA)

Em geral, essas simetrias são profundamente importantes para nossa compreensão do Universo e têm enormes implicações adicionais para a realidade. Veja bem, há um teorema brilhante na interseção da física e da matemática que afirma o seguinte: toda simetria matemática única exibida por uma teoria física necessariamente implica uma quantidade conservada associada. Este teorema - conhecido como teorema de Noether depois de seu descobridor, o incomparável matemático Emmy Noether – é a raiz de por que certas quantidades são ou não conservadas.

Uma simetria de translação no tempo leva à conservação de energia, o que explica por que energia é não conservada em um universo em expansão . A simetria de translação espacial leva à conservação do momento; simetria rotacional leva à conservação do momento angular. Até Conservação CPT — onde a conjugação de carga, a paridade e a simetria de reversão no tempo são todas combinadas — é uma consequência da simetria de Lorentz.

A gravidade quântica tenta combinar a teoria geral da relatividade de Einstein com a mecânica quântica. As correções quânticas à gravidade clássica são visualizadas como diagramas de loop, como o mostrado aqui em branco. Se o espaço (ou o tempo) em si é discreto ou contínuo ainda não está decidido, assim como a questão se a gravidade é quantizada ou se as partículas, como as conhecemos hoje, são fundamentais ou não. Mas se esperamos uma teoria fundamental de tudo, ela deve incluir campos quantizados. (LAC ACELERADOR LABORATÓRIO NACIONAL)

Algumas simetrias são inerentes a QFTs específicos ou a QFTs em geral; algumas simetrias são inerentes a soluções específicas em GR ou a GR em geral. Mas essas duas descrições do Universo são incompletas. Há muitas perguntas que podemos fazer sobre a realidade que exigem que entendamos o que está acontecendo onde a gravidade é importante ou onde a curvatura do espaço-tempo é extremamente forte (onde precisamos de GR), mas também quando as escalas de distância são muito pequenas ou onde os efeitos quânticos individuais são em jogo (onde precisamos de QFT).

Isso inclui perguntas como as seguintes :

• O que acontece com o campo gravitacional de um elétron quando ele passa por uma fenda dupla?
• O que acontece com a informação das partículas que formam um buraco negro, se o estado eventual do buraco negro é radiação térmica?
• E qual é o comportamento de um campo/força gravitacional em e ao redor de uma singularidade?

Para abordá-los, GR e QFT individualmente são insuficientes. Precisamos de algo mais: uma compreensão da gravidade no nível quântico.

Um holograma é uma superfície bidimensional que contém informações sobre todo o objeto tridimensional exibido codificado nela. A ideia do princípio holográfico é que nosso Universo e as leis teóricas do campo quântico que o descrevem são a superfície de um espaço-tempo de dimensão superior que inclui a gravidade quântica. (GEORG-JOHANN LAY / EPZCAW / E. SIEGEL (DOMÍNIO PÚBLICO))

Não temos uma teoria funcional da gravidade quântica, é claro, ou seríamos capazes de entender quais simetrias ela exibe (e não exibe). Mas mesmo sem uma teoria completa, temos uma pista tremenda: o princípio holográfico. Assim como um holograma bidimensional codifica informações tridimensionais em sua superfície, o princípio holográfico permite que os físicos relacionem o que acontece em um espaço-tempo com N dimensões para uma teoria de campo conforme com N-1 dimensões: a correspondência AdS/CFT .

O AdS significa espaço anti-de Sitter, que é frequentemente usado para descrever a gravidade quântica no contexto da teoria das cordas, enquanto o CFT significa teoria de campo conforme, como os QFTs que usamos para descrever três das quatro interações fundamentais. Embora ninguém tenha certeza se isso é aplicável ao nosso Universo, existem muitas boas razões para pensar que sim .

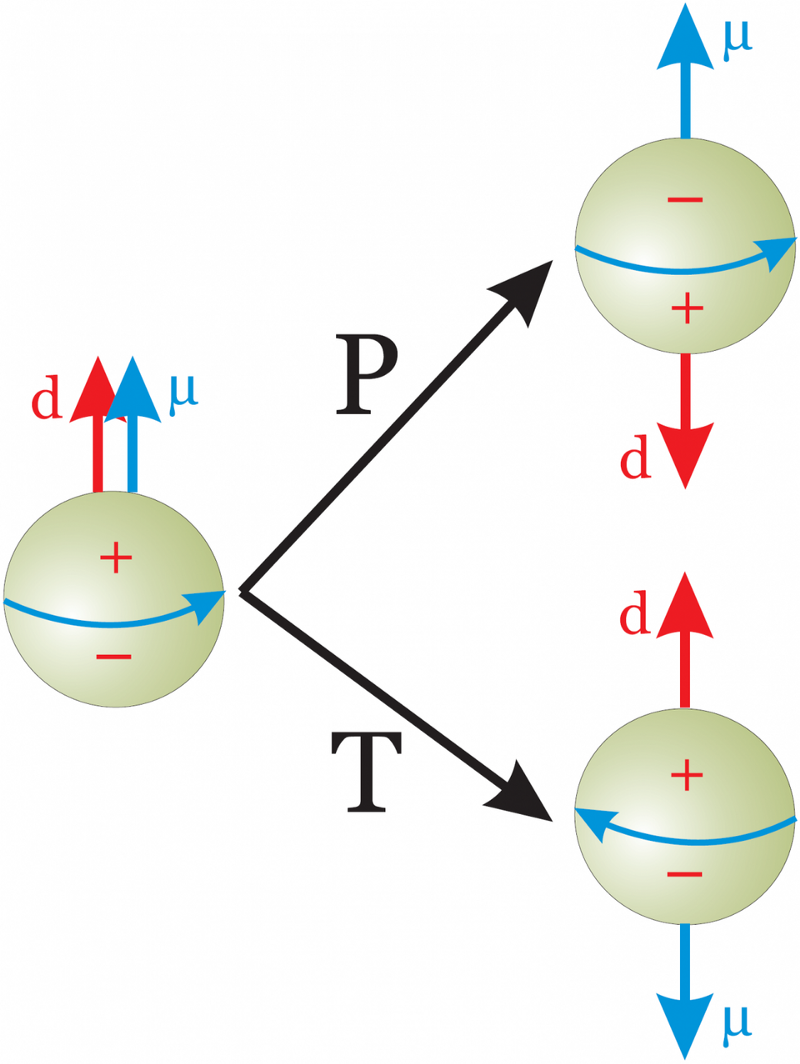
No Modelo Padrão, prevê-se que o momento de dipolo elétrico do nêutron seja um fator de dez bilhões maior do que nossos limites observacionais mostram. A única explicação é que, de alguma forma, algo além do Modelo Padrão está protegendo essa simetria CP nas interações fortes. Podemos demonstrar muitas coisas na ciência, mas provar que o CP é conservado nas interações fortes nunca pode ser feito. O que é muito ruim; precisamos de mais violação de CP para explicar a assimetria matéria-antimatéria presente em nosso Universo. Não pode haver simetrias globais se a correspondência AdS/CFT estiver correta. (TRABALHO DE DOMÍNIO PÚBLICO DE ANDREAS KNECHT)

O novo resultado, que é muito abrangente em suas implicações, é este: dentro da estrutura de AdS/CFT, não há simetrias globais . O próprio artigo, publicado em 17 de maio de 2019, é intitulado Restrições nas Simetrias da Holografia e foi escrito por Daniel Harlow e Hirosi Ooguri. Em particular, mostrou que – novamente, no contexto da AdS/CFT – que as três conjecturas a seguir são verdadeiras.

1. A gravidade quântica não permite simetrias globais de nenhum tipo.
2. A gravidade quântica requer que qualquer simetria interna de calibre (o que implica em leis de conservação como carga elétrica, carga de cor ou isospin fraco) seja matematicamente compacta.
3. A gravidade quântica requer que qualquer simetria interna de calibre necessariamente venha junto com objetos dinâmicos que se transformam em todas as representações irredutíveis.

Cada um deles merece elaboração, mas o primeiro é o mais poderoso e profundo.

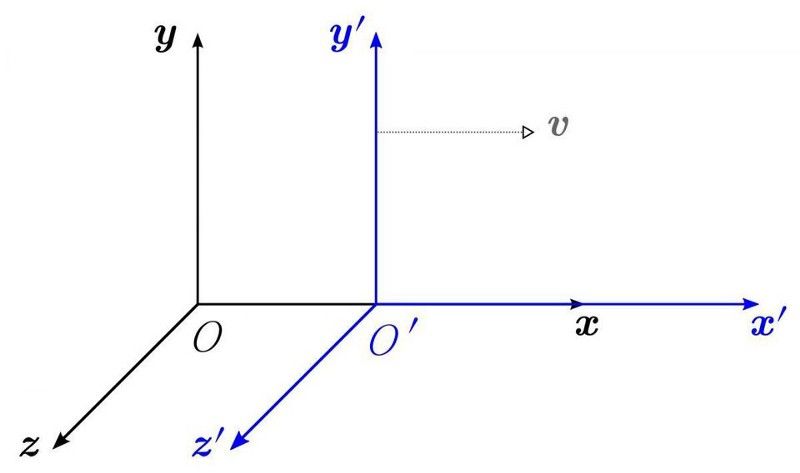
Diferentes quadros de referência, incluindo diferentes posições e movimentos, veriam diferentes leis da física (e discordariam da realidade) se uma teoria não fosse relativisticamente invariante. O fato de termos uma simetria sob ‘aumentos’, ou transformações de velocidade, nos diz que temos uma quantidade conservada: momento linear. Isso é muito mais difícil de compreender quando o momento não é simplesmente uma quantidade associada a uma partícula, mas sim um operador da mecânica quântica. Essa simetria, se o princípio holográfico estiver correto, não pode existir globalmente. (WIKIMEDIA COMMONS USUÁRIO KREA)

Todas essas três conjecturas existem há muito tempo, e nenhuma delas é estritamente verdadeira em QFT ou GR (ou qualquer forma de física clássica) por conta própria. Os argumentos clássicos para todos eles, de fato, estão enraizados na física dos buracos negros e são conhecidos por exigir certas suposições que, se violadas, admitem várias brechas. Mas se a correspondência AdS/CFT for verdadeira e o princípio holográfico for aplicável à gravidade quântica em nosso Universo, todas essas três conjecturas são válidas.

A primeira significa que não há leis de conservação que sempre necessariamente se apliquem. Pode haver bom aproximado leis de conservação que ainda são válidas, mas nada — nem energia, nem momento angular, nem momento linear — é explicitamente ou estritamente conservado em todas as condições. Mesmo a invariância CPT e Lorentz pode ser violada. Os outros dois são mais sutis, mas ajudam a estender as simetrias globais às condições locais: eles impedem coisas como o teletransporte instantâneo de carga elétrica de um local para outro, local desconectado, e exigem a existência de todas as cargas possíveis permitidas pela teoria, como como monopolos magnéticos.

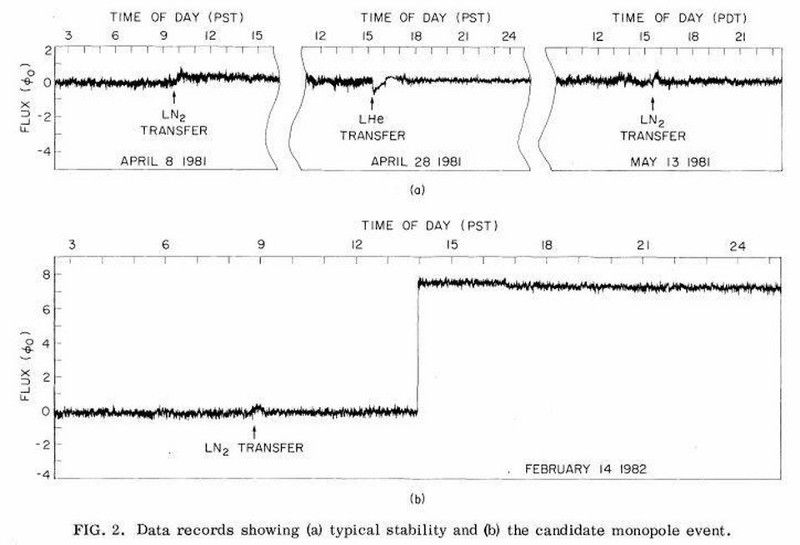
Em 1982, um experimento conduzido por Blas Cabrera, um com oito espiras de fio, detectou uma mudança de fluxo de oito magnetons: indícios de um monopolo magnético. Infelizmente, ninguém estava presente no momento da detecção e ninguém jamais reproduziu esse resultado ou encontrou um segundo monopolo. Ainda assim, se a teoria das cordas e esse novo resultado estiverem corretos, os monopolos magnéticos, não sendo proibidos por nenhuma lei, devem existir em algum nível. (CABRERA B. (1982). PRIMEIROS RESULTADOS DE UM DETECTOR SUPERCONDUTIVO PARA MONÓPOLES MAGNÉTICOS EM MOVIMENTO, CARTAS DE REVISÃO FÍSICA, 48 (20) 1378–1381)

As três conjecturas da gravidade quântica que são comprovadas para um universo holográfico já existem, de alguma forma, desde 1957 , mas eram apenas conjecturas até agora. Se o princípio holográfico (e AdS/CFT, e possivelmente a teoria das cordas, por extensão) estiver correto, todas essas conjecturas são necessariamente verdadeiras. Não há simetrias globais; nada no Universo é sempre conservado em todas as circunstâncias imagináveis ​​(mesmo que você precise para atingir a escala de Planck para ver violações), e todas as cobranças não proibidas devem existir. Seria revolucionário para nossa compreensão do Universo quântico.

Apesar dos resultados e implicações deste estudo, ele ainda é limitado. Não sabemos se o princípio holográfico é verdadeiro ou não, ou se essas suposições sobre a gravidade quântica estão corretas. Se estiver certo, no entanto, significa que, uma vez que você inclua a gravidade, muitas das simetrias que consideramos tão caras na física que conhecemos hoje não são globais e fundamentais. Paradoxalmente, se a teoria das cordas estiver certa, nossas expectativas sobre simetrias ocultas que se revelam em um nível mais fundamental não estão apenas erradas, mas a natureza não tem simetrias globais.

Atualizar : O primeiro autor do artigo, Daniel Harlow, estendeu a mão para esclarecer um ponto que não foi suficientemente apreciado pelo autor. Ele relata o seguinte:

Eu queria salientar que há um problema técnico em sua descrição… nosso teorema não se aplica a nenhuma das simetrias que você menciona aqui! E, de fato, no AdS/CFT, todos eles podem ser ininterruptos. A razão é que todos eles são, na verdade, simetrias de medida, não simetrias globais. Para carga elétrica, acho que você está familiarizado com isso, mas na teoria gravitacional, como a relatividade geral, as traduções, transformações de Lorentz, CPT, etc. também são simetrias de calibre: são apenas difeomorfismos.

A diferença entre uma simetria de calibre e uma simetria global é que a presença de carga de calibre pode ser medida de longe, enquanto a presença de uma carga global não pode. Por exemplo, no eletromagnetismo, se quisermos saber a carga total em uma região, basta medir o fluxo elétrico através de sua fronteira. Da mesma forma, na gravidade, se quisermos saber a energia de algo, podemos medir a queda da métrica distante (basicamente procurando o M na métrica de Schwarzschild). Isso deve ser comparado, por exemplo, com a simetria global Z_2 do modelo de Ising, onde não há como saber se os spins estão em alta em uma região sem ir lá e olhar para eles.

Não é muito apreciado, mas no modelo padrão da física de partículas acoplada à gravidade existe apenas uma simetria global: aquela descrita pela conservação de B-L (número bariônico menos número leptônico). Portanto, esta é a única simetria conhecida que estamos dizendo que deve ser violada!

Envie suas perguntas Ask Ethan para beginwithabang no gmail ponto com !

Começa com um estrondo é agora na Forbes , e republicado no Medium graças aos nossos apoiadores do Patreon . Ethan é autor de dois livros, Além da Galáxia , e Treknology: A ciência de Star Trek de Tricorders a Warp Drive .

Compartilhar: