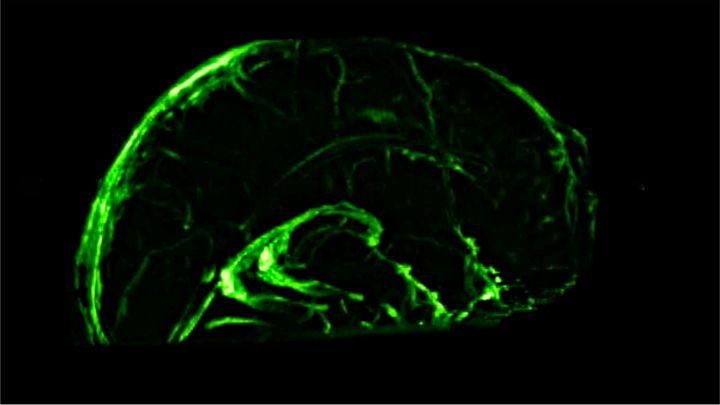
Sim, partículas virtuais podem ter efeitos reais e observáveis
À medida que as ondas eletromagnéticas se propagam para longe de uma fonte cercada por um forte campo magnético, a direção de polarização será afetada devido ao efeito do campo magnético no vácuo do espaço vazio: birrefringência do vácuo. Ao medir os efeitos dependentes do comprimento de onda da polarização em torno de estrelas de nêutrons com as propriedades corretas, podemos confirmar as previsões de partículas virtuais no vácuo quântico. (N. J. SHAVIV / SCIENCEBITS)
A natureza do nosso Universo quântico é intrigante, contra-intuitiva e testável. Os resultados não mentem.
Embora nossa intuição seja uma ferramenta incrivelmente útil para navegar na vida diária, desenvolvida a partir de uma vida inteira de experiência em nossos próprios corpos na Terra, muitas vezes é horrível fornecer orientação fora desse reino. Em escalas muito grandes e muito pequenas, nos saímos muito melhor aplicando nossas melhores teorias científicas, extraindo previsões físicas e depois observando e medindo os fenômenos críticos.
Sem essa abordagem, nunca teríamos entendido os blocos básicos de construção da matéria, o comportamento relativista da matéria e da energia ou a natureza fundamental do espaço e do tempo em si. Mas nada combina com a natureza contra-intuitiva do vácuo quântico. O espaço vazio não é completamente vazio, mas consiste em um estado indeterminado de campos e partículas flutuantes. Não é ficção científica; é uma estrutura teórica com previsões testáveis e observáveis. 80 anos depois que Heisenberg postulou pela primeira vez um teste observacional, a humanidade o confirmou. Aqui está o que aprendemos.
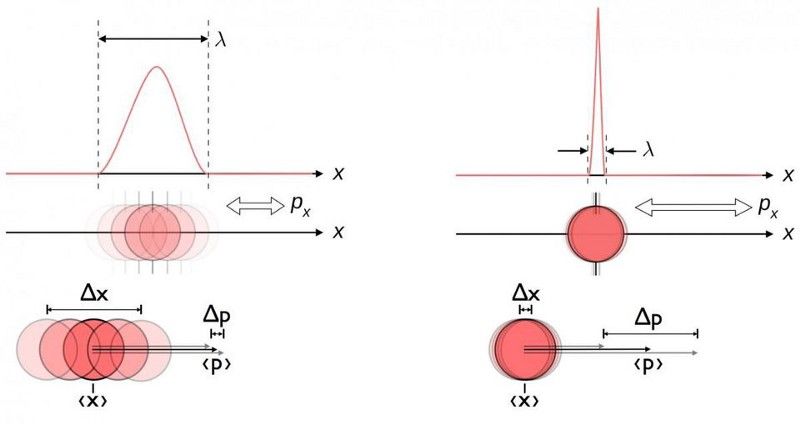
Uma ilustração entre a incerteza inerente entre posição e momento no nível quântico. Há um limite para o quão bem você pode medir essas duas quantidades simultaneamente, e a incerteza aparece em lugares onde as pessoas geralmente menos esperam. (E. SIEGEL / WIKIMEDIA COMMONS USUÁRIO MASCHE)
Descobrir que nosso Universo era de natureza quântica trouxe consigo muitas consequências não intuitivas. Quanto melhor você mediu a posição de uma partícula, mais fundamentalmente indeterminado era seu momento. Quanto mais curta uma partícula instável vivia, menos conhecida sua massa era fundamentalmente. Objetos materiais que parecem sólidos em escalas macroscópicas podem exibir propriedades semelhantes a ondas sob as condições experimentais corretas.
Mas o espaço vazio talvez seja o primeiro lugar quando se trata de um fenômeno que desafia nossa intuição. Mesmo se você remover todas as partículas e radiação de uma região do espaço – ou seja, todas as fontes de campos quânticos – o espaço ainda não estará vazio. Será composto por pares virtuais de partículas e antipartículas, cuja existência e espectros de energia podem ser calculados. Enviar o sinal físico correto através desse espaço vazio deve ter consequências observáveis.

Uma ilustração do Universo primitivo como consistindo de espuma quântica, onde as flutuações quânticas são grandes, variadas e importantes nas menores escalas. (NASA/CXC/M.WEISS)
As próprias partículas que existem temporariamente no vácuo quântico podem ser virtuais, mas seu efeito sobre a matéria ou a radiação é muito real. Quando você tem uma região do espaço pela qual as partículas passam, as propriedades desse espaço podem ter efeitos físicos reais que podem ser previstos e testados.
Um desses efeitos é este: quando a luz se propaga no vácuo, se o espaço estiver perfeitamente vazio, ela deve se mover por esse espaço sem impedimentos: sem dobrar, desacelerar ou quebrar em vários comprimentos de onda. A aplicação de um campo magnético externo não muda isso, pois os fótons, com seus campos elétricos e magnéticos oscilatórios, não se curvam em um campo magnético. Mesmo quando seu espaço está preenchido com pares de partículas/antipartículas, esse efeito não muda. Mas se você aplicar um forte campo magnético a um espaço preenchido com pares de partículas/antipartículas, de repente surge um efeito real e observável.
Visualização de um cálculo da teoria quântica de campos mostrando partículas virtuais no vácuo quântico. (Especificamente, para as interações fortes.) Mesmo no espaço vazio, essa energia do vácuo é diferente de zero. À medida que os pares partícula-antipartícula surgem e desaparecem, eles podem interagir com partículas reais como elétrons ou fótons, deixando assinaturas impressas nas partículas reais que são potencialmente observáveis. (DEREK LEINWEBER)
Quando você tem pares de partículas/antipartículas presentes no espaço vazio, você pode pensar que eles simplesmente surgem, vivem por um tempo e depois re-aniquilam e voltam ao nada. No espaço vazio sem campos externos, isso é verdade: o princípio da incerteza de energia-tempo de Heisenberg se aplica e, desde que todas as leis de conservação relevantes ainda sejam obedecidas, isso é tudo o que acontece.
Mas quando você aplica um campo magnético forte, partículas e antipartículas têm cargas opostas uma da outra. Partículas com as mesmas velocidades, mas cargas opostas, se curvarão em direções opostas na presença de um campo magnético, e a luz que passa por uma região do espaço com partículas carregadas que se movem dessa maneira específica deve exibir um efeito: deve ser polarizada. Se o campo magnético for forte o suficiente, isso deve levar a uma polarização observável grande, em uma quantidade que depende da força do campo magnético.

Houve muitas tentativas de medir o efeito da birrefringência do vácuo em um ambiente de laboratório, como com uma configuração de pulso de laser direto, como mostrado aqui. No entanto, eles não tiveram sucesso até agora, pois os efeitos foram muito pequenos para serem vistos com campos magnéticos terrestres, mesmo com raios gama na escala GeV. (YOSHIHIDE NAKAMIYA, KENSUKE HOMMA, TOSEO MORITAKA, E KEITA SETO, VIA ARXIV.ORG/ABS/1512.00636 )
Esse efeito é conhecido como birrefringência a vácuo, ocorrendo quando partículas carregadas são puxadas em direções opostas por fortes linhas de campo magnético. Mesmo na ausência de partículas, o campo magnético induzirá esse efeito apenas no vácuo quântico (ou seja, no espaço vazio). O efeito desta birrefringência de vácuo fica mais forte muito rapidamente à medida que a força do campo magnético aumenta: como o quadrado da força do campo. Mesmo que o efeito seja pequeno, temos lugares no Universo onde as forças do campo magnético são grandes o suficiente para tornar esses efeitos relevantes.
O campo magnético natural da Terra pode ser apenas ~ 100 microtesla, e os campos mais fortes feitos pelo homem ainda são apenas cerca de 100 T. Mas as estrelas de nêutrons nos dão a oportunidade para condições particularmente extremas, dando-nos grandes volumes de espaço onde a força do campo excede 10⁸ ( 100 milhões) T, condições ideais para medir a birrefringência a vácuo.

Uma estrela de nêutrons, apesar de ser composta principalmente de partículas neutras, produz os campos magnéticos mais fortes do Universo, um quatrilhão de vezes mais fortes do que os campos na superfície da Terra. Quando as estrelas de nêutrons se fundem, elas devem produzir ondas gravitacionais e também assinaturas eletromagnéticas e, quando cruzam um limiar de cerca de 2,5 a 3 massas solares (dependendo do spin), podem se tornar buracos negros em menos de um segundo. (NASA / CASEY REED — PENN STATE UNIVERSITY)
Como as estrelas de nêutrons criam campos magnéticos tão grandes? A resposta pode não ser o que você pensa. Embora possa ser tentador usar o nome “estrela de nêutrons” literalmente, ele não é feito exclusivamente de nêutrons. Os 10% externos de uma estrela de nêutrons consistem principalmente de prótons, núcleos leves e elétrons, que podem existir de forma estável sem serem esmagados na superfície da estrela de nêutrons.
As estrelas de nêutrons giram extremamente rapidamente, frequentemente acima de 10% da velocidade da luz, o que significa que essas partículas carregadas nos arredores da estrela de nêutrons estão sempre em movimento, o que exigiu a produção de correntes elétricas e campos magnéticos induzidos. Esses são os campos que devemos procurar se quisermos observar a birrefringência do vácuo e seu efeito na polarização da luz.
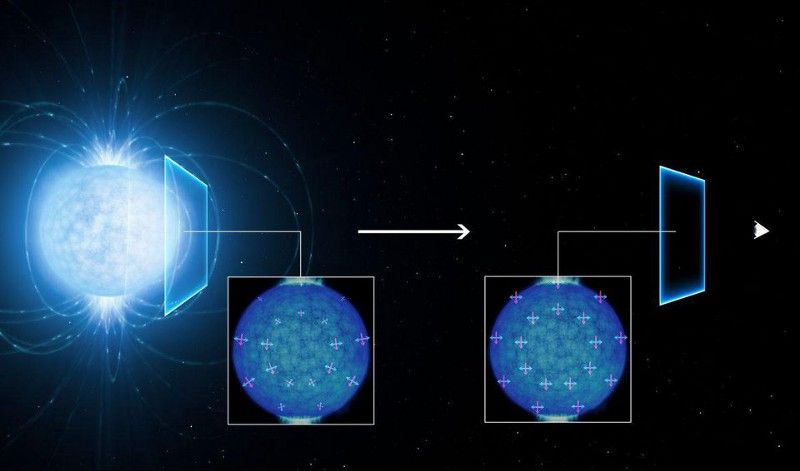
A luz vinda da superfície de uma estrela de nêutrons pode ser polarizada pelo forte campo magnético pelo qual passa, graças ao fenômeno da birrefringência do vácuo. Detectores aqui na Terra podem medir a rotação efetiva da luz polarizada. (ESO/L. CALÇADA)
É um desafio medir a luz das estrelas de nêutrons: embora sejam bastante quentes, mais quentes até do que as estrelas normais, são minúsculas, com diâmetros de apenas algumas dezenas de quilômetros. Uma estrela de nêutrons é como uma estrela brilhante semelhante ao Sol, talvez duas ou três vezes a temperatura do Sol, comprimida em um volume do tamanho de Washington, D.C.
As estrelas de nêutrons são muito fracas, mas emitem luz de todo o espectro, incluindo até a parte de rádio do espectro. Dependendo de onde escolhemos olhar, podemos observar os efeitos dependentes do comprimento de onda que o efeito da birrefringência do vácuo tem na polarização da luz.

Imagem do VLT da área ao redor da estrela de nêutrons muito fraca RX J1856.5–3754. O círculo azul, adicionado por E. Siegel, mostra a localização da estrela de nêutrons. Observe que, apesar de aparecer muito fraca e vermelha nesta imagem, há luz suficiente chegando aos nossos detectores para que, com a instrumentação adequada, procuremos esse efeito de birrefringência do vácuo. (ISSO)
Toda a luz emitida deve passar pelo forte campo magnético ao redor da estrela de nêutrons a caminho de nossos olhos, telescópios e detectores. Se o espaço magnetizado pelo qual ela passa exibe o efeito de birrefringência do vácuo esperado, essa luz deve ser toda polarizada, com uma direção comum de polarização para todos os fótons.
Em 2016, os cientistas conseguiram localizar uma estrela de nêutrons que estava perto o suficiente e possuía um campo magnético forte o suficiente para tornar essas observações possíveis. Trabalhando com o Very Large Telescope (VLT) no Chile, que pode fazer fantásticas observações ópticas e infravermelhas, incluindo polarização, uma equipe liderada por Roberto Mignani conseguiu medir o efeito de polarização da estrela de nêutrons RX J1856.5-3754.
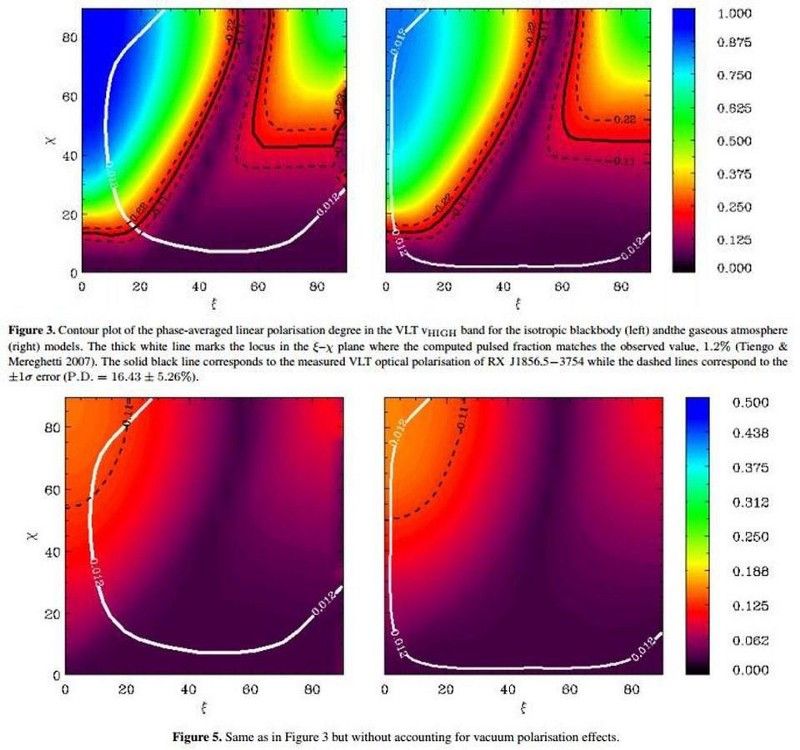
Um gráfico de contorno do grau de polarização linear com média de fase em dois modelos (esquerda e direita): para um corpo negro isotrópico e para um modelo com atmosfera gasosa. Na parte superior, você pode ver os dados observacionais, enquanto na parte inferior, você pode ver o que obtém se subtrair o efeito teórico da birrefringência do vácuo dos dados. Os efeitos combinam parcialmente perfeitamente. (R.P. MIGNANI ET AL., MNRAS 465, 492 (2016))
Os autores conseguiram extrair, dos dados, um grande efeito: um grau de polarização em torno de 15%. Eles também calcularam qual deveria ser o efeito teórico da birrefringência do vácuo e o subtraíram dos dados reais medidos. O que eles descobriram foi espetacular: o efeito teórico da birrefringência do vácuo foi responsável por praticamente toda a polarização observada. Em outras palavras, os dados e as previsões combinaram quase perfeitamente.
Você pode pensar que um pulsar mais próximo e mais jovem (como o da Nebulosa do Caranguejo) pode ser mais adequado para fazer tal medição, mas há uma razão pela qual o RX J1856.5-3754 é especial: sua superfície não é obscurecida por uma densa , magnetosfera cheia de plasma.
Se você observar um pulsar como o da Nebulosa do Caranguejo, poderá ver os efeitos da opacidade na região ao seu redor; simplesmente não é transparente à luz que queremos medir.
Mas a luz ao redor do RX J1856.5–3754 é simplesmente perfeita. Com as medidas de polarização nesta porção do espectro eletromagnético deste pulsar, temos a confirmação de que a luz é, de fato, polarizada na mesma direção das previsões decorrentes da birrefringência do vácuo na eletrodinâmica quântica. Essa é a confirmação de um efeito previsto há tanto tempo — em 1936 — por Werner Heisenberg e Hans Euler que, décadas após a morte dos dois homens, podemos agora acrescentar astrofísico teórico a cada um de seus currículos.

O futuro observatório de raios X da ESA, Athena, incluirá a capacidade de medir a polarização da luz de raios X do espaço, algo que nenhum dos nossos principais observatórios atuais, como Chandra e XMM-Newton, pode fazer. (COLABORAÇÃO ESA / ATENA)
Agora que o efeito da birrefringência do vácuo foi observado – e por associação, o impacto físico das partículas virtuais no vácuo quântico – podemos tentar confirmá-lo ainda mais com medições quantitativas mais precisas. A maneira de fazer isso é medir RX J1856.5-3754 nos raios X e medir a polarização da luz de raios X.
Embora não tenhamos um telescópio espacial capaz de medir a polarização de raios-X no momento, um deles está em andamento: a missão Athena da ESA. Ao contrário da polarização de ~15% observada pelo VLT nos comprimentos de onda que ele sonda, os raios X devem ser totalmente polarizados, exibindo cerca de 100% de efeito. Atualmente, o Athena está programado para ser lançado em 2028 e pode fornecer essa confirmação não apenas para uma, mas para muitas estrelas de nêutrons. É mais uma vitória para o universo quântico não intuitivo, mas inegavelmente fascinante.
Começa com um estrondo é agora na Forbes , e republicado no Medium graças aos nossos apoiadores do Patreon . Ethan é autor de dois livros, Além da Galáxia , e Treknology: A ciência de Star Trek de Tricorders a Warp Drive .
Compartilhar: