• Começa Com Um Estrondo

Pergunte a Ethan: Como as partículas sem massa experimentam a gravidade?

Esta imagem ilustra um efeito de lente gravitacional e os vários caminhos que a luz pode seguir para chegar ao mesmo destino. Dadas as grandes distâncias cósmicas e enormes massas em jogo, os tempos de chegada podem diferir em horas ou décadas entre as imagens, mas a própria luz está claramente experimentando os efeitos da gravidade, embora não tenha massa própria. (NASA, ESA E JOHAN RICHARD (CALTECH, EUA); AGRADECIMENTOS: DAVIDE DE MARTIN & JAMES LONG (ESA/HUBBLE))

A explicação de Einstein é a única que funciona.

Quando Newton propôs pela primeira vez a lei da gravitação universal, marcou a primeira vez que percebemos que a mesma regra que rege como os objetos caem na Terra também governa como eles se movem e se atraem por todo o Universo. Objetos caíram na Terra por causa da gravidade; A Terra puxa-se para um esferóide por causa da gravidade; luas orbitam planetas e planetas orbitam o Sol por causa da gravidade; e assim por diante em escalas cada vez maiores. A lei de Newton era simples, mas profunda: objetos com massa se atraem dependendo apenas de suas massas, distâncias e da constante gravitacional do Universo. Então, como partículas sem massa, como fótons, experimentam a gravidade? É isso que Bret Hammers quer saber, perguntando:

Dada a equação da gravidade entre duas massas e o fato de que os fótons não têm massa, como é possível que uma massa (como uma estrela ou um buraco negro) exerça influência sobre o referido fóton?

É uma pergunta muito boa, mas que nossa compreensão mais profunda da gravidade pode responder. Vamos ver como.

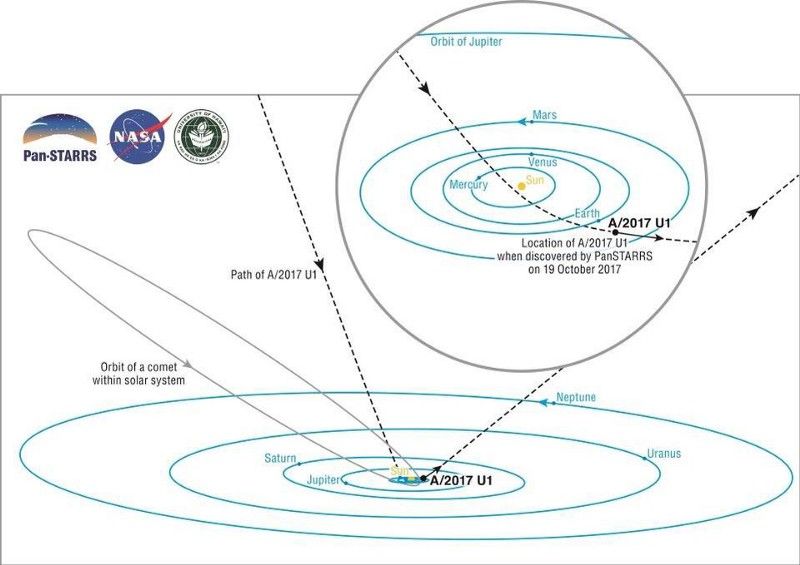
Este diagrama esquemático do nosso sistema solar mostra o caminho dramático de A/2017 U1 (linha tracejada) quando cruzou o plano dos planetas (conhecido como eclíptica), e depois virou e voltou. A órbita hiperbólica de alguns objetos que não estão ligados, as órbitas elípticas e circulares de corpos ligados e as formas parabólicas que objetos em queda traçam em um campo gravitacional são exemplos do que você chega a partir de uma simples lei de força newtoniana. (BROOKS BAYS / SOEST PUBLICATION SERVICES / UH INSTITUTE FOR ASTRONOMY)

Quando Newton apareceu, sua concepção de gravidade era radicalmente revolucionária. As pessoas já haviam medido como os objetos aceleravam perto da superfície da Terra, com a distância que eles caíam aumentando proporcionalmente ao tempo em que estavam caindo ao quadrado. Kepler revolucionou a astronomia ao demonstrar que os planetas orbitavam o Sol em uma órbita elíptica. E Halley, um contemporâneo de Newton, começou a entender a natureza periódica dos cometas.

Newton, incrivelmente, foi capaz de sintetizar tudo isso em uma única estrutura. Os objetos caíram na mesma velocidade que na Terra porque aceleraram em direção ao centro da Terra. As luas orbitavam seus planetas por causa da atração mútua; mesmo com planetas e cometas orbitando o Sol. Uma lei simples, direta e simples: a constante gravitacional multiplicada por duas massas quaisquer, dividida pela distância ao quadrado entre elas, fornece a força gravitacional.

A lei da gravitação universal de Newton foi substituída pela relatividade geral de Einstein, mas baseou-se no conceito de uma ação instantânea (força) à distância e é incrivelmente direta. A constante gravitacional nesta equação, G, juntamente com os valores das duas massas e a distância entre elas, são os únicos fatores na determinação de uma força gravitacional. (USUÁRIO WIKIMEDIA COMMONS DENNIS NILSSON)

Isso explicava todos os diferentes tipos de órbitas possíveis: círculos, elipses, parábolas e hipérboles. Explicava a energia potencial gravitacional e como essa energia potencial se transformaria em energia cinética. Isso explicou a velocidade de escape e nos permitiu eventualmente descobrir como escapar das ligações gravitacionais da Terra. Se houvesse um problema envolvendo a força gravitacional, a gravidade newtoniana poderia resolvê-lo. Por cerca de 200 anos, explicou tudo o que já observamos.

O raciocínio por trás disso também era tão simples: se você pudesse afirmar, com certeza e precisão,

• o que todas as massas no Universo eram em um determinado momento,
• onde estavam localizados,
• e como eles estavam se movendo inicialmente,

A gravidade de Newton poderia dizer qual seria a força em cada objeto em todo o Universo em qualquer momento. O Universo, de acordo com Newton, era completamente determinista.

As órbitas dos planetas e cometas, entre outros objetos celestes, são regidas pelas leis da gravitação universal. (KAY GIBSON, BALL AEROSPACE & TECHNOLOGIES CORP)

Aqui está a ideia básica de um universo newtoniano: você tem todas as suas massas que existem, elas se atraem, instantaneamente, em qualquer distância do espaço, para todo o tempo, com exatamente a magnitude que a lei da gravitação universal de Newton prevê. Isso é verdade para todas as massas em todos os lugares em todos os momentos. Se isso fosse 100%, imutavelmente verdade, não haveria como reconciliar isso com a luz sendo dobrada pela massa. A luz não tem massa ( m = 0) e, portanto, todas as massas em todo o Universo não podem exercer nenhuma força sobre ele. Qualquer coisa, não importa quão grande, multiplicada por 0 ainda é igual a 0.

Mas a imagem de Newton não pode estar certa, e a Relatividade Especial de Einstein ilustra o porquê. Imagine que você e eu estamos um ao lado do outro e, quando uma arma de partida dispara, você corre para a frente, para a frente, enquanto eu tropeço e permaneço em repouso. Quando olhamos para uma massa distante, nos atraindo, você vê fisicamente uma distância diferente daquela massa do que eu, mesmo que ainda estejamos no mesmo local no espaço.

Um desafio para a teoria newtoniana foi a ideia, apresentada por Einstein, mas anteriormente construída por Lorentz, Fitzgerald e outros, de que objetos em movimento rápido pareciam se contrair no espaço e dilatar no tempo. Espaço e tempo, de repente, não pareciam tão fixos e absolutos. (CURT RENHAW)

A razão para isso é a contração do comprimento, que afirma que os observadores que se movem em velocidades diferentes discordam sobre as distâncias observadas: quanto mais rápido você for, mais curtos (mais contraídos) os comprimentos parecerão. Esta é apenas uma consequência da relatividade, mas ilustra muito bem por que a imagem newtoniana não pode ser verdadeira.

Aquela massa distante que você e eu vemos – com um de nós parado e o outro em movimento – exercerá uma força gravitacional em nós dois. Se estivermos à mesma distância desse objeto, fisicamente, a força de atração deve ser a mesma. Mas se a distância é relativa, então quem está correto? Minha medição estacionária para as distâncias da massa até nós está correta? Ou sua medição em movimento para a medição, que é menor, está correta?

Na imagem newtoniana da gravidade, espaço e tempo são quantidades absolutas e fixas, enquanto na imagem einsteiniana, o espaço-tempo é uma estrutura única e unificada onde as três dimensões do espaço e a dimensão única do tempo estão inextricavelmente ligadas. (NASA)

A resposta, surpreendentemente, é que ambos precisamos estar corretos. Uma lei da gravidade correta deve ser correta para quem a observa, e a imagem de Newton é incompatível com isso. Demorou até 1915 para que uma formulação mais correta surgisse, e essa foi a chegada da Relatividade Geral de Einstein.

Conceitualmente, a relatividade de Einstein não se parece muito com a imagem de Newton. Em particular, afirma as seguintes diferenças principais.

• Espaço e tempo são relativos, não absolutos e fixos, e a visão de cada observador deles é igualmente válida.
• A entidade do espaço-tempo é deformada (ou geometricamente curvada) por todas as tensões sobre ela.
• A causa da deformação do espaço-tempo não é apenas a massa, mas todos os tipos de energia somados, onde a massa é apenas uma forma de energia.
• E essas mudanças na curvatura do espaço-tempo só podem se propagar na velocidade da gravidade (que é igual à velocidade da luz), não instantaneamente.

Na teoria da gravidade de Newton, as órbitas fazem elipses perfeitas quando ocorrem em torno de grandes massas únicas. No entanto, na Relatividade Geral, há um efeito de precessão adicional devido à curvatura do espaço-tempo, e isso faz com que a órbita se desloque ao longo do tempo, de uma forma que às vezes é mensurável. Mercúrio sofre precessão a uma taxa de 43″ (onde 1″ é 1/3600 de um grau) por século; o buraco negro menor em OJ 287 precessa a uma taxa de 39 graus por órbita de 12 anos. (NCSA, UCLA / KECK, A. GHEZ GROUP; VISUALIZAÇÃO: S. LEVY E R. PATTERSON / UIUC)

Então, Einstein está certo? Newton está certo? Cada um deles está parcialmente certo?

A razão pela qual a relatividade de Einstein foi proposta em primeiro lugar foi que havia um problema na gravidade newtoniana: ela falhou em prever corretamente a mudança do movimento da órbita do planeta Mercúrio ao longo do tempo. Havia uma contribuição adicional necessária, e Einstein sabia que estava em algo profundo, finalmente, quando sua teoria foi capaz de reproduzir esses pequenos desvios da teoria de Newton.

Mas precisava haver um teste adicional – onde as duas ideias concorrentes fizessem previsões diferentes – que pudesse diferenciá-las uma da outra.

Uma antiga placa fotográfica de estrelas (circulada) identificada durante um eclipse solar em 1900. (ESPAÇO CHABOT & CENTRO DE CIÊNCIAS)

O primeiro teste crítico foi usar o próprio Sol e ver se ele dobrava a luz ou não. Aqueles de vocês que viram o eclipse solar total de 2017 podem ter notado uma estrela, Regulus, a apenas cerca de um grau do Sol eclipsado. As estrelas são visíveis durante muitos eclipses, e seu caminho pode parecer passar muito perto do objeto mais massivo do Sistema Solar: o nosso Sol. Mas essa luz se curvaria? Estas foram as três ideias:

1. Se Newton estivesse correto, e apenas massas fossem atraídas, então a luz não se curvaria; a deflexão angular aparente seria zero.
2. Se Newton estivesse parcialmente certo e sua lei fosse verdadeira, mas você precisasse atribuir aos fótons uma massa efetiva (porque eles têm uma energia, e sabemos que E = mc² ), então você pode atribuir a eles uma massa de m = E/c² , e calcule uma deflexão angular aparente.
3. Ou, se Einstein estivesse totalmente certo, você precisaria usar sua nova teoria da Relatividade Geral para calcular a deflexão angular aparente, o que lhe dá uma figura duas vezes maior que a deflexão semi-newtoniana anterior.

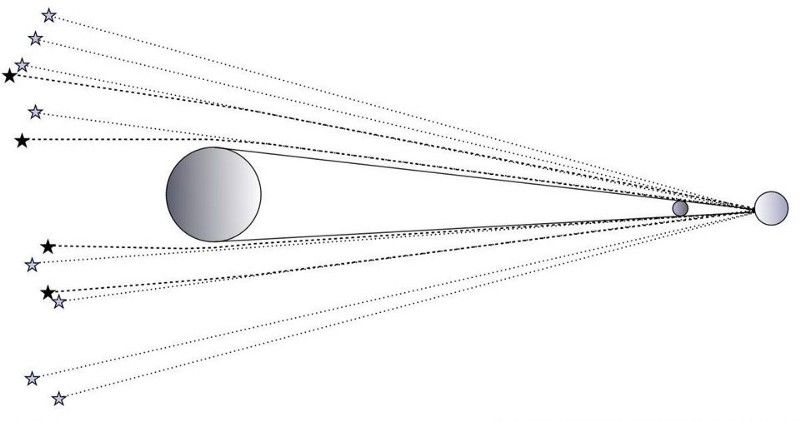
Durante um eclipse total, as estrelas parecem estar em uma posição diferente de suas localizações reais, devido à curvatura da luz de uma massa intermediária: o Sol. (E. SIEGEL / ALÉM DA GALÁXIA)

O eclipse solar total de 1919 teve vários observadores em todo o mundo para fazer exatamente essas medições críticas. Conhecida hoje como a expedição de Eddington, em homenagem ao astrônomo britânico Arthur Eddington que idealizou o teste observacional, os dados foram coletados dos continentes sul-americano e africano e reunidos para análise.

Quando a análise foi concluída, mesmo quando os erros foram incluídos, a conclusão foi clara: houve uma deflexão da luz das estrelas e foi consistente com as previsões de Einstein. A teoria da gravidade de Newton não descreve o Universo; você precisa da Relatividade Geral de Einstein para acertar.

Os resultados da expedição de Eddington de 1919 mostraram, de forma conclusiva, que a Teoria Geral da Relatividade descrevia a curvatura da luz das estrelas em torno de objetos massivos, derrubando a imagem newtoniana. Esta foi a primeira confirmação observacional da Relatividade Geral de Einstein e parece estar alinhada com a visualização do “tecido do espaço dobrado”. (THE ILUSTRADO LONDRES NEWS, 1919)

Hoje, temos um século de retrospectiva em relação à Relatividade Geral e à gravidade newtoniana. Sabemos que em quase todas as circunstâncias – contanto que você não esteja muito perto de uma massa muito grande – a gravidade newtoniana é uma excelente aproximação à nossa melhor teoria da gravidade. Mas se você quiser ser mais correto, precisará levar em conta esses efeitos normalmente pequenos. O desvio da luz das estrelas de uma linha reta durante o eclipse solar de 1919 foi de apenas 0,0005°, mas conseguimos medi-lo com a precisão necessária.

Em vez de uma grade 3D vazia, em branco, colocar uma massa para baixo faz com que o que seriam linhas “retas” se tornem curvas por uma quantidade específica. Na Relatividade Geral, tratamos o espaço e o tempo como contínuos, mas todas as formas de energia, incluindo, mas não se limitando à massa, contribuem para a curvatura do espaço-tempo. (CHRISTOPHER VITALE DAS REDES E O INSTITUTO PRATT)

As massas não são o único árbitro da atração gravitacional; todas as formas de energia contribuem e são afetadas. A quantidade pela qual eles são afetados é apenas aproximadamente newtoniana e, onde as diferenças são grandes, a teoria de Einstein concorda com o que observamos. A matéria e a energia curvam o espaço-tempo, e o espaço-tempo curvo dizem tanto à matéria quanto à energia como se mover. É por isso que as massas podem exercer uma influência gravitacional nos fótons: elas curvam o espaço. O fóton não tem escolha do que precisa fazer. Ele se move em linha reta a partir de sua perspectiva; não pode ajudar se o próprio Universo, porque contém matéria e energia, não é feito de linhas retas!

Envie suas perguntas Ask Ethan para beginwithabang no gmail ponto com !

Começa com um estrondo é agora na Forbes , e republicado no Medium graças aos nossos apoiadores do Patreon . Ethan é autor de dois livros, Além da Galáxia , e Treknology: A ciência de Star Trek de Tricorders a Warp Drive .

Compartilhar: