Pergunte a Ethan #36: O Incrível Elétron Giratório

Mesmo adicionar apenas uma partícula extra faz toda a diferença.
A arte tem uma maneira de nos confrontar, de nos lembrar, de nos engajar, no que significa ser humano, e o que significa ser humano é ser falho, é ser contraditório, é ser frequentemente fraco e, no entanto, apesar tudo isso que consideramos inconvenientes, que também somos muito bonitos. O giro é o oposto. – Junot Diaz
É o final da semana aqui no Starts With A Bang, e isso significa que é hora de outra coluna Ask Ethan. Você tem enviado seu perguntas e sugestões a semana inteira e – como prometido – escolhi o meu favorito para compartilhar com você e responder para todo o mundo. A pergunta desta semana vem de Bill Galloway, que pergunta:
Enquanto eu lia seu resposta em laser lembrou-me de uma pergunta que tenho há muito tempo sobre o princípio de exclusão de Pauli. Eu não sou um físico, então minhas desculpas se eu não estou fazendo a pergunta corretamente. Meu entendimento é que os dois elétrons em uma molécula de hidrogênio têm que ter spins opostos. Então, o spin dos elétrons muda à medida que eles formam uma molécula ou só é possível que átomos de hidrogênio com spins opostos formem uma molécula?
Há muito encapsulado na pergunta de Bill, então vamos começar com o Princípio de Exclusão de Pauli .

Crédito da imagem: Fermilab, modificado por mim.
Apesar da enorme diversidade dos diferentes tipos de partículas fundamentais que existem no Universo – como evidenciado pelo Modelo Padrão, acima – todas elas podem ser divididas em dois tipos:
- Férmions ou partículas com spin semi-inteiro: ±1/2, ±3/2, ±5/2, etc.
- Bósons ou partículas com spin inteiro: 0, ±1, ±2, etc.
O que é incrível é que composto as partículas se comportam como férmions ou bósons também, com seus amigos familiares o próton e o nêutron se comportando como férmions com spins de ± 1/2, assim como os elétrons. Cada partícula tem um certo conjunto de estados quânticos pode ocupar com níveis discretos de energia, valores de momento angular, direções de rotação, etc.
E a principal diferença entre férmions e bósons é que se você tem dois idêntico partículas, você pode colocar quantos bósons quiser no mesmo estado quântico, mas férmions idênticos são excluído de ocupar exatamente o mesmo estado.

Crédito de imagem: UC Davis ChemWiki, via http://chemwiki.ucdavis.edu/Physical_Chemistry/Quantum_Mechanics/Atomic_Theory/Electrons_in_Atoms/Electronic_Orbitals , sob c.c.-by-3.0.
Se o elétron não eram um férmion (e em vez disso fosse um bóson), então sempre que você tivesse um átomo, você poderia empacotar quantos elétrons quisesse no estado de energia mais baixo (em vermelho, acima) quanto quisesse! Mas o elétron é um férmion, e assim é sujeito à regra de exclusão de Pauli. O estado de energia mais baixo pode aceitar dois elétrons, porque um pode ser spin +1/2 e o outro pode ser spin -1/2, mas se você adicionar um terceiro elétron, você precisa pular para um estado quântico diferente.
E a maneira como os estados quânticos funcionam nos átomos é que você pode passar para um estado de energia mais alto (indicado por n , abaixo), e depois para estados de momento angular progressivamente mais altos ( eu , abaixo).

Crédito da imagem: Departamento de Química do Beloit College, via http://chemlinks.beloit.edu/Stars/pages/orbitals.html .
Então o eu = 0 estados são os orbitais s, os eu = 1 estados são os orbitais p, o eu = 2 estados são os orbitais d, e assim por diante. Isto é Por quê a tabela periódica dos elementos tem a estrutura que se observa: com 2 elementos na linha superior (preenchendo n =1, l = 0, m =0 e spin = ±1/2), 8 elementos na segunda linha ( n =2, l = 0, m =0, e rotação = ±1/2, e n =2, l=1, m =1,0 ou -1 e spin = ±1/2), 18 elementos na terceira linha ( n =3, l = 0, m =0 e rotação = ±1/2; n =3, l=1, m =1,0, ou -1 e spin = ±1/2; e n =3, l=2, m =2,1,0,-1 ou -2 e rotação = ±1/2), etc.
Crédito da imagem: Todd Helmenstine e Anne Marie Helmenstine, via http://chemistry.about.com/od/periodictables/ig/Printable-Periodic-Tables/Color-Periodic-Table.htm .
Então, quando você vê a tabela periódica, obtenha um extra 6, 10, 14, etc., entradas a cada nova linha , o princípio de exclusão de Pauli é o motivo!
Mesmo que não tenhamos como distinguir um elétron do outro (porque eles são idêntico ), cada sistema atômico é exclusivo . Em outras palavras, se eu tiver quatro átomos de hidrogênio diferentes no estado fundamental, eles são não vai ser obrigado a ocupar diferentes estados de energia.
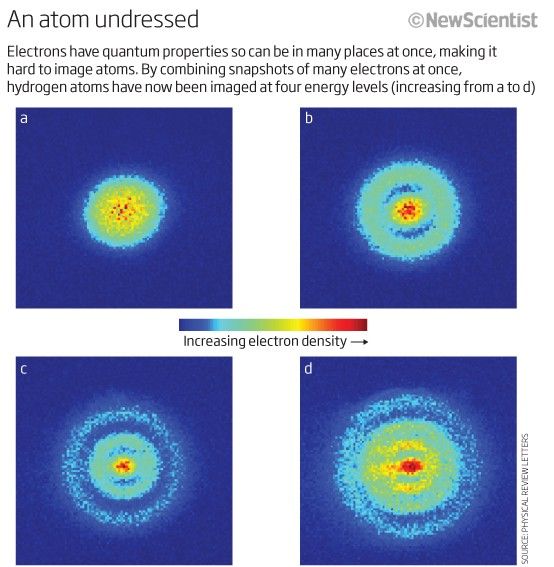
Crédito da imagem: New Scientist.
Na verdade, porque os núcleos atômicos (os prótons) são distintos um do outro (ou seja, não estão no mesmo núcleo, ou em um estado quântico sobreposto em qualquer sentido), e os elétrons estão ligados ao seu próprio próton pai (ou seja, não em estados quânticos sobrepostos um com o outro), um sistema de átomos de hidrogênio livres muito provavelmente teria todos eles no estado fundamental, para algo parecido com isso.
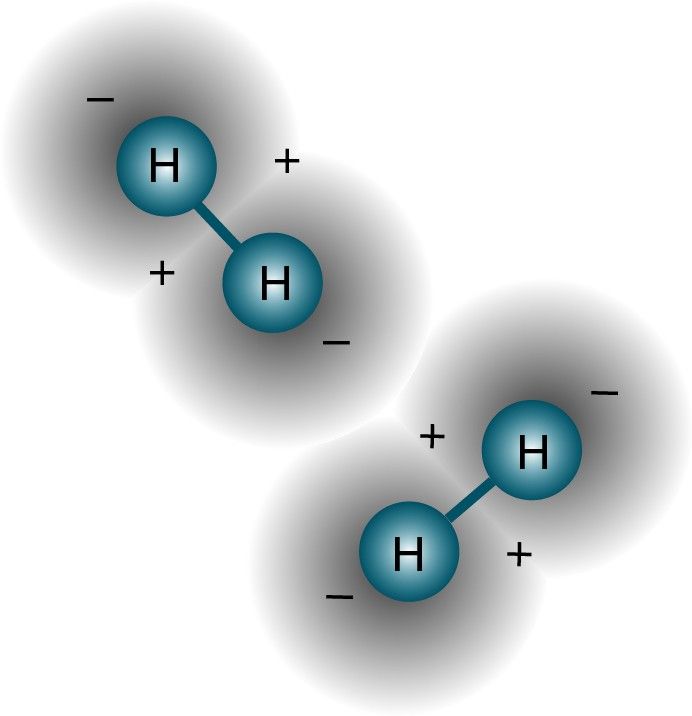
Crédito da imagem: eu, modificado a partir da imagem acima.
Pelo menos, essa é uma maneira razoável de configurar seu sistema inicialmente. Mas se dois desses átomos de hidrogênio entrarem em contato um com o outro, eles vão querer se ligar e formar uma molécula de hidrogênio. Afinal, assim como um átomo de hidrogênio no estado fundamental é um pouco mais leve – 13,6 eV mais leve - do que um próton livre e um elétron livre devido à energia de ligação , uma molécula de hidrogênio também é um pouco mais leve - por 4,52 eV — do que dois átomos de hidrogênio livres.
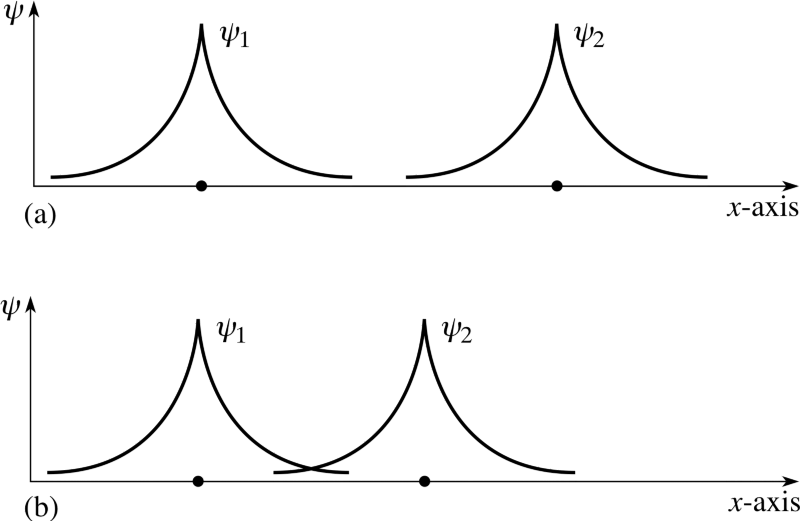
Mas você está certo em se preocupar com esses elétrons idêntico estados. Porque uma vez que esses dois átomos separados tentam se unir, as funções de onda dos elétrons Faz tente e sobreponha!

Crédito da imagem: Copyright do material FLAP 1996 Open University, via http://www.met.reading.ac.uk/pplato2/h-flap/phys11_4.html .
Mas lembre-se que os elétrons são mais do que apenas partículas com rodar sozinho; eles também tem espacial funções de onda, que é uma maneira elegante de dizer que ocupam o espaço de uma maneira particular. Se eu aproximar dois átomos de hidrogênio, suas funções de onda espaciais podem ser simétrico , como mostra o diagrama acima, ou podem ser anti-simétrico , como mostrado no diagrama abaixo.

Crédito da imagem: Copyright do material FLAP 1996 Open University, via http://www.met.reading.ac.uk/pplato2/h-flap/phys11_4.html .
Agora, é aqui que entra a regra de exclusão de Pauli, e é fascinante.
Se os dois átomos de hidrogênio entrarem com simétrico funções de onda, então os spins dos elétrons devem ser anti -aligned: se o primeiro foi +1/2, o segundo deve ser -1/2, e se o primeiro foi -1/2, o segundo deve ser +1/2.
Da mesma forma, se os dois átomos vierem com antisimétrico funções de onda, então os spins dos elétrons devem ser similarmente -aligned: se o primeiro for +1/2, o segundo deve ser +1/2, e se o primeiro for -1/2, o segundo também deve ser -1/2!
Então, se perguntarmos como dois átomos de hidrogênio podem ser configurados juntos, existem duas configurações possíveis: ou em um estado espacialmente simétrico, mas anti-alinhado por spin, ou em um estado anti-simétrico espacialmente, mas alinhado por spin!
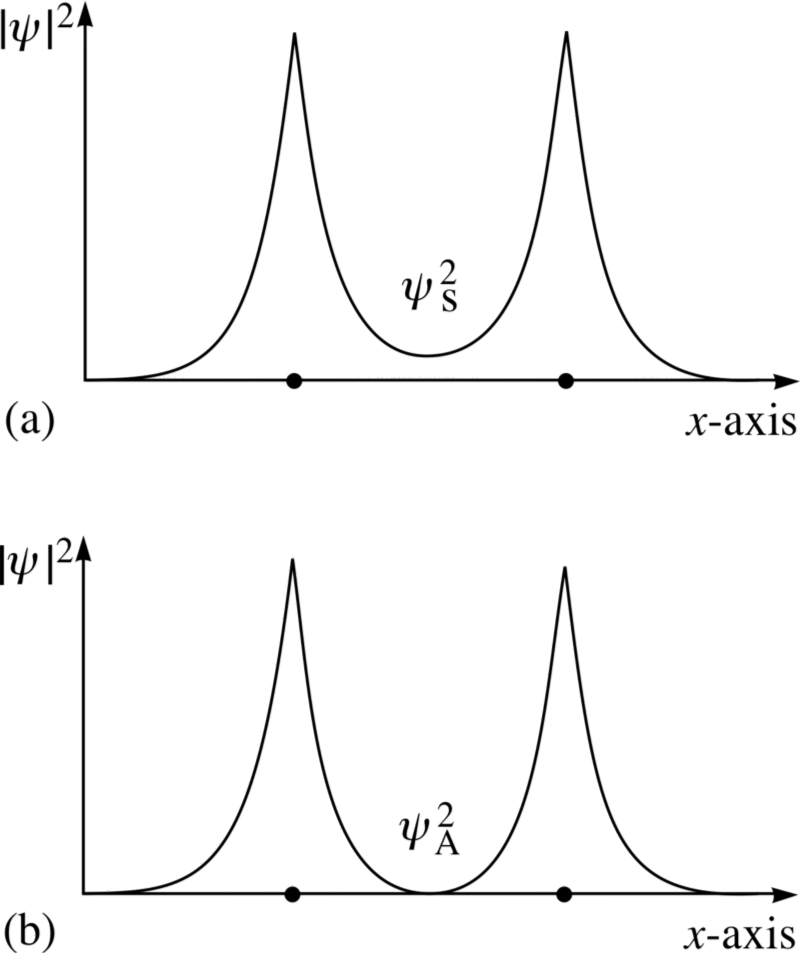
Crédito da imagem: Copyright do material FLAP 1996 Open University, via http://www.met.reading.ac.uk/pplato2/h-flap/phys11_4.html .
Veja essas duas combinações; para o de cima, as funções de onda sobreposição , indicando uma ligação, enquanto para a inferior, as funções de onda não se sobrepõem, nos dizendo que este é um anti - estado de ligação!
Podemos realmente calcular - quantitativamente, se quisermos - como é a energia de ligação para esses dois estados.

Crédito das imagens: R. Nave de http://hyperphysics.phy-astr.gsu.edu/hbase/molecule/hmol.html .
O estado anti-simétrico, onde os spins dos elétrons estão alinhados uns com os outros, não ligue ; apenas o estado simétrico, onde as funções de onda espaciais são simétricas, mas os spins são anti-alinhados, pode formar uma molécula de hidrogênio ligada!
Portanto, você não precisa apenas de dois átomos de hidrogênio com funções de onda espaciais simétricas e rotações opostas (+1/2 e -1/2) para formar uma molécula de hidrogênio, mas também pode ver claramente como a mecânica quântica proíbe você de obter um terceiro hidrogênio aí sempre , e é por isso que você pode ter um átomo H, a molécula H2, mas você pode Nunca tem H3 ou superior!

Crédito da imagem: CERN, 2001, via http://www.physicsmasterclasses.org/exercises/keyhole/it/theory/main-5.html .
E é assim que a mecânica quântica permite que você forme uma molécula de hidrogênio, mas apenas em circunstâncias muito específicas! Obrigado por uma ótima pergunta, Bill, e se você quiser ver sua pergunta ou sugestão respondida no Ask Ethan da próxima semana, envie o seu aqui por uma chance!
Deixe um comentário em o fórum Starts With A Bang em Scienceblogs !
Compartilhar:
















