• Começa Com Um Estrondo

Em um universo quântico, mesmo a massa é incerta

Faixas da câmara de bolhas do Fermilab, revelando a carga, massa, energia e momento das partículas criadas. Se uma partícula recém-criada não for estável a tempos de vida arbitrários, ela terá uma incerteza inerente à sua massa. (FNAL/NSF/DOE)

No mundo quântico do instável, mesmo partículas idênticas não têm massas idênticas.

No mundo microscópico da partícula quântica, existem certas regras que nos são totalmente desconhecidas em escala macroscópica. Se você medir a posição de uma partícula e perguntar onde você está, quanto mais precisamente você aprender a resposta, você saberá fundamentalmente seu movimento, ou seu momento, menos bem. Outras propriedades, no entanto, como a carga elétrica, permanecem perfeitamente conhecidas em todos os momentos, independentemente do que mais você mede. Para partículas puramente estáveis, sejam elementares ou compostas (incluindo elétrons e prótons), a massa é uma dessas propriedades perfeitamente conhecidas. Se você conhece a massa de um elétron sob um conjunto de condições, você a conhece para todos os elétrons em todo o Universo. Mas este não é o caso de todas as partículas que conhecemos. Quanto mais curta for uma partícula instável, mais incerta será sua massa. Este não é apenas um efeito hipotético, mas sim um que foi observado e verificado experimentalmente por décadas.

A natureza quântica do Universo nos diz que certas quantidades têm uma incerteza inerente embutida nelas, e que pares de quantidades têm suas incertezas relacionadas umas às outras. (NASA/CXC/M.Weiss)

Do ponto de vista teórico, a incerteza quântica deve desempenhar um papel sempre que existirem duas propriedades físicas relacionadas de uma certa maneira. Essa relação em particular é aquela que chamamos de não comutativa, e é estranho pensar nisso. Se eu medir sua posição (onde você está), por exemplo, e depois medir seu momento (uma medida de seu movimento), você esperaria que eu obtivesse os mesmos resultados que se eu medisse primeiro seu momento e depois seu posição. Na física clássica, todas as variáveis ​​comutam: não importa se você mede a posição e depois o momento, ou o momento e depois a posição. Você obtém as mesmas respostas de qualquer maneira. Mas na física quântica, há uma incerteza inerente que surge, e medir a posição e o momento é fundamentalmente diferente de medir o momento e depois a posição.

Uma visualização do QCD ilustra como os pares partícula/antipartícula saem do vácuo quântico por períodos de tempo muito pequenos como consequência da incerteza de Heisenberg. Se você tiver uma grande incerteza na energia (ΔE), o tempo de vida (Δt) da(s) partícula(s) criada(s) deve ser muito curto. (Derek B. Leinweber)

É como se eu lhe dissesse que 3 + 4 era de alguma forma fundamentalmente diferente de 4 + 3. No universo quântico, isso é um propriedade fundamental e inevitável conhecida como incerteza de Heisenberg , e informa que para quantidades como posição (Δ x ) e momento (Δ p ), há essa incerteza inerente entre eles e, portanto, uma incerteza inerente em cada variável. Isso também não se restringe à posição e ao momento. Existem muitas quantidades físicas por aí - muitas vezes para razões esotéricas na física quântica - que têm essa mesma relação de incerteza entre eles. Isso acontece para cada par de variáveis ​​conjugadas temos, assim como a posição e o momento. Eles incluem:

• Energia (Δ E ) e tempo (Δ t ),
• Potencial elétrico, ou tensão (Δ Phi ) e carga elétrica livre (Δ que ),
• Momento angular (Δ eu ) e orientação, ou posição angular (Δ θ ),

junto com muitos outros. Ele diz que essas duas quantidades, multiplicadas juntas, devem ser maiores ou iguais a algum valor finito: ℏ/2.

Uma ilustração entre a incerteza inerente entre posição e momento no nível quântico. (E. Siegel / usuário do Wikimedia Commons Maschen)

Embora a posição e o momento sejam os exemplos usuais sobre os quais falamos, neste caso, é a relação energia e tempo que leva ao comportamento bizarro e confuso. Se uma partícula é completamente estável, então a incerteza em sua vida não importa: qualquer incerteza finita (Δ t ) adicionado a um tempo de vida infinito é irrelevante. Mas se uma partícula é instável, há uma incerteza em quanto tempo ela sobrevive que é aproximadamente igual ao seu tempo de vida médio: Δ t . Isso significa que também há uma incerteza inerente à sua energia; usando nossa fórmula de incerteza, ela nos diz que se você multiplicar sua incerteza de energia (Δ E ) pela sua incerteza de tempo (Δ t ), deve ser maior ou igual a ℏ/2.

E quanto menor for o tempo de vida de sua partícula, maior sua incerteza de energia precisa ser.

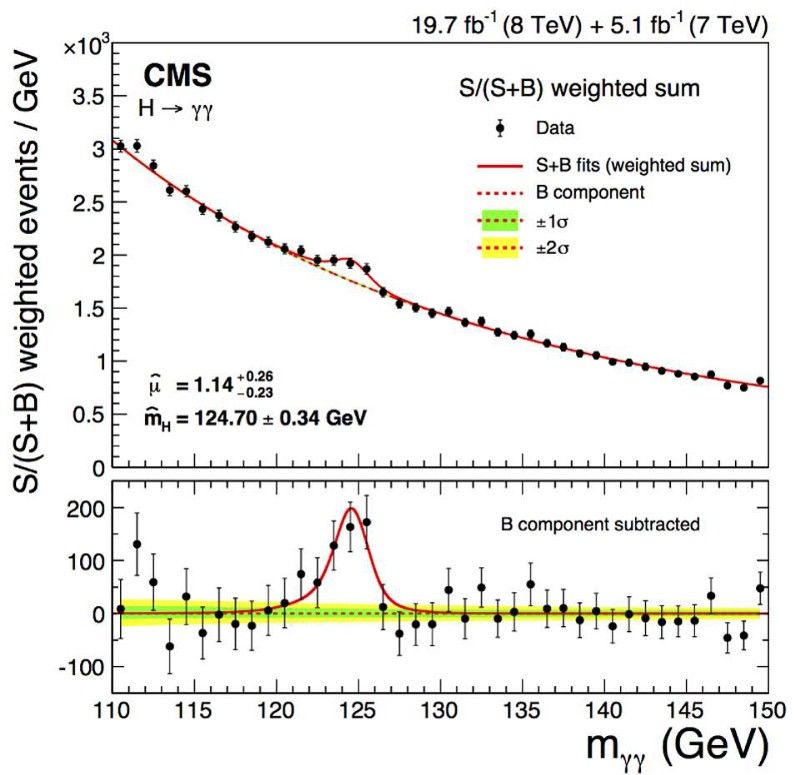
A primeira detecção robusta de 5 sigma do bóson de Higgs foi anunciada há alguns anos pelas colaborações CMS e ATLAS. Mas o bóson de Higgs não faz um único “pico” nos dados, mas sim um aumento espalhado, devido à sua incerteza inerente na massa. (A Colaboração CMS, Observação do decaimento de difótons do bóson de Higgs e medição de suas propriedades, (2014))

Mas uma incerteza na energia, para uma partícula, significa que também deve haver uma incerteza inerente à sua massa, uma vez que E = mc² . Se ela tiver uma incerteza de energia maior, ela terá uma incerteza de massa maior, e quanto mais curta for uma partícula, maior será sua incerteza de massa. Muitas pessoas notaram, quando detectaram o bóson de Higgs pela primeira vez, que ele apareceu como um aumento nos dados (acima). Se o bóson de Higgs fosse, em vez disso, sempre a mesma massa exata e única, nós o reconstruiríamos como um pico infinitamente estreito, onde a única incerteza vinha de nossas próprias medições.

A largura inerente, ou metade da largura do pico na imagem acima quando você está a meio caminho do topo, é medida em 2,5 GeV: uma incerteza inerente de cerca de +/- 3% da massa total. (Colaboração ATLAS (Schieck, J. pela colaboração) JINST 7 (2012) C01012)

Agora, é verdade que existem incertezas de medição/detector, e elas desempenham um papel. Mas muitas partículas – como o bóson de Higgs, o bóson Z, os bósons W+ e W- e o quark top – têm vida incrivelmente curta, com tempos de vida na ordem de 10^-24 segundos! (Ou, no caso do quark top, ainda menos que isso.) Toda vez que você cria uma partícula de Higgs, ela pode ser (em termos de energia) 124,5 GeV, 125,0 GeV, 125,5 GeV ou 126,0 GeV, ou qualquer coisa entre . Quando você cria um bóson Z, ele pode variar de cerca de 88 GeV a 94 GeV. E, mais notavelmente, quando você cria um quark top, ele pode ter uma massa de repouso de cerca de 165 GeV até mais de 180 GeV: a maior faixa de qualquer partícula elementar conhecida.

As distribuições de massa reconstruídas dos quarks top no detector CDF no Fermilab, antes da ativação do LHC, mostraram uma grande incerteza na massa do quark top. Embora a maior parte disso tenha ocorrido devido às incertezas do detector, há uma incerteza inerente à própria massa que aparece como parte desse pico amplo. (S. Shiraishi, J. Adelman, E. Brubaker, Y.K. Kim pela colaboração do CDF)

Isso significa que, literalmente, quando você cria uma dessas partículas e mede quanta energia ela tinha, é fundamentalmente e inerentemente diferente da próxima partícula. exatamente do mesmo tipo você vai criar. Esta é uma propriedade não intuitiva das partículas quânticas que só surge quando são instáveis. Qualquer elétron que você cria é indistinguível de qualquer outro elétron no Universo, mas cada quark top que existe terá seu próprio conjunto único de partículas e energias que decaem a partir dele, com uma incerteza inerente a todas as suas propriedades, incluindo sua massa total /energia.

As massas das partículas fundamentais podem ser quantificadas, incluindo os neutrinos, mas apenas as partículas que são verdadeiramente estáveis ​​podem ter uma massa exata atribuída a elas. Caso contrário, é apenas a massa “média” que pode ser afirmada com alguma certeza. (Hitoshi Murayama de http://hitoshi.berkeley.edu/)

É um dos resultados mais notáveis ​​e contra-intuitivos do Universo quântico, que cada partícula instável que você faz tem uma incerteza inerente à propriedade aparentemente mais fundamental de todas: a massa. Você pode saber qual é a massa média de uma partícula típica de qualquer tipo específico e pode medir sua largura, que está diretamente relacionada ao seu tempo de vida médio através do princípio da incerteza de Heisenberg. Mas toda vez que você cria uma nova partícula, não há como saber qual será sua massa real; tudo o que você pode fazer é calcular as probabilidades de ter uma variedade de massas. Para saber com certeza, tudo o que você pode fazer é medir o que sai e reconstruir o que realmente existiu. A incerteza quântica, vista pela primeira vez para a posição e o momento, agora pode ser afirmada de forma convincente para se estender até a energia de repouso de uma partícula fundamental. Em um universo quântico, mesmo a própria massa não é imutável.

Começa com um estrondo é agora na Forbes , e republicado no Medium graças aos nossos apoiadores do Patreon . Ethan é autor de dois livros, Além da Galáxia , e Treknology: A ciência de Star Trek de Tricorders a Warp Drive .

Compartilhar: