• Começa com um estrondo

Não, nosso Universo não é feito de matemática pura

A menos que você confronte sua teoria com o que realmente existe no Universo, você está jogando na caixa de areia, não se envolvendo com a ciência.

Principais conclusões

• Chegamos a muitas ideias, algumas das quais são fisicamente relevantes para nossa realidade, por meio de ideação puramente matemática.
• No entanto, a matemática sozinha não vai pintar um quadro preciso da realidade; devemos conciliar o que 'pensamos' com o que podemos observar e medir.
• Brincar na caixa de areia é bom, mas reconheça o que realmente é: brincadeira matemática. Se você quer realidade, enfrente o próprio Universo.

Ethan Siegel Compartilhe Não, nosso Universo não é feito de matemática pura no Facebook Compartilhar Não, nosso Universo não é feito de matemática pura Twitter Compartilhar Não, nosso universo não é feito de matemática pura no LinkedIn

Nas fronteiras da física teórica, muitas das ideias mais populares têm uma coisa em comum: elas partem de uma estrutura matemática que busca explicar mais coisas do que nossas teorias predominantes atualmente. Nossas estruturas atuais para Relatividade Geral e Teoria Quântica de Campos são ótimas para o que fazem, mas não fazem tudo. Eles são fundamentalmente incompatíveis entre si e não podem explicar suficientemente a matéria escura, a energia escura ou a razão pela qual nosso Universo é preenchido com matéria e não antimatéria, entre outros quebra-cabeças.

É verdade que a matemática nos permite descrever quantitativamente o Universo, é uma ferramenta incrivelmente útil quando aplicada corretamente. Mas o Universo é uma entidade física, não matemática, e há uma grande diferença entre os dois. É por isso que a matemática sozinha sempre será insuficiente para chegar a uma teoria fundamental de tudo.

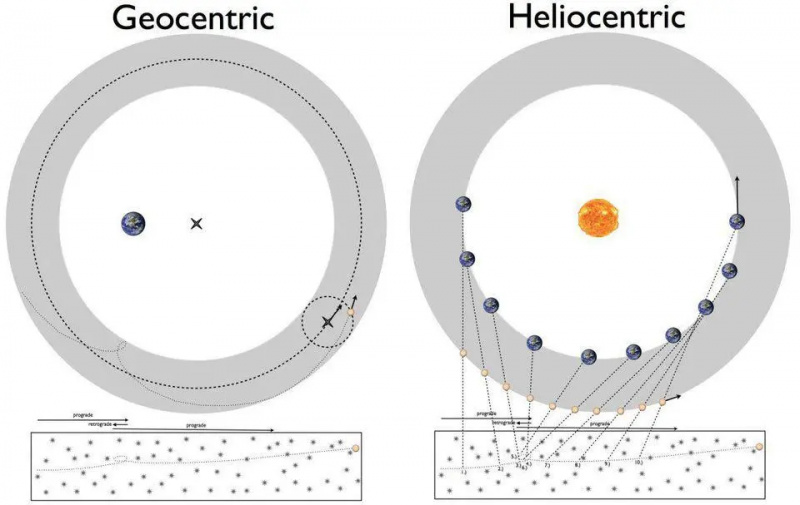Um dos grandes quebra-cabeças dos anos 1500 era como os planetas se moviam de maneira aparentemente retrógrada. Isso pode ser explicado pelo modelo geocêntrico de Ptolomeu (à esquerda) ou pelo modelo heliocêntrico de Copérnico (à direita). No entanto, acertar os detalhes com precisão arbitrária era algo que exigiria avanços teóricos em nossa compreensão das regras subjacentes aos fenômenos observados, o que levou às leis de Kepler e, eventualmente, à teoria da gravitação universal de Newton.

Cerca de 400 anos atrás, uma batalha estava se desenrolando sobre a natureza do Universo. Por milênios, os astrônomos descreveram com precisão as órbitas dos planetas usando um modelo geocêntrico, onde a Terra estava estacionária e todos os outros objetos orbitavam ao seu redor. Armado com a matemática da geometria e observações astronômicas precisas - incluindo ferramentas como círculos, equantes, deferentes e epiciclos - a descrição matemática precisa das órbitas dos corpos celestes correspondeu ao que vimos de forma espetacular.

A combinação não foi perfeita, no entanto, e as tentativas de melhorá-la levaram a mais epiciclos ou, no século XVI, ao heliocentrismo de Copérnico. Ao colocar o Sol no centro, as explicações do movimento retrógrado tornaram-se mais simples, mas os ajustes aos dados foram piores. Quando Johannes Kepler apareceu, ele teve uma ideia brilhante que buscava resolver tudo.

O modelo original de Kepler do Sistema Solar, o Mysterium Cosmographicum, consistia nos 5 sólidos platônicos definindo os raios relativos de 6 esferas, com os planetas orbitando em torno das circunferências dessas esferas. Por mais bonito que seja, não poderia descrever o Sistema Solar tão bem quanto as elipses, ou mesmo tão bem quanto o modelo de Ptolomeu.

Ele notou que havia seis planetas no total, se você incluísse a Terra, mas não a Lua da Terra. Ele também notou que, matematicamente, havia apenas cinco sólidos platônicos: cinco objetos matemáticos cujas faces são polígonos de lados iguais. Ao desenhar uma esfera dentro e fora de cada um, ele poderia “aninhá-los” de uma forma que se ajustasse extremamente bem às órbitas planetárias: melhor do que qualquer coisa que Copérnico havia feito. Foi um modelo matemático brilhante e bonito e, sem dúvida, a primeira tentativa de construir o que poderíamos chamar de “um universo elegante” hoje.

Mas, observacionalmente, falhou. Ele falhou em ser tão bom quanto o antigo modelo ptolomaico com seus epiciclos, equantes e deferentes. Foi uma ideia brilhante e a primeira tentativa de argumentar — apenas com base na matemática pura — como o Universo deveria ser. Mas simplesmente não funcionou.

O que veio a seguir foi um golpe de gênio que definiria o legado de Kepler.

A segunda lei de Kepler afirma que os planetas varrem áreas iguais, usando o Sol como um foco, em tempos iguais, independentemente de outros parâmetros. A mesma área (azul) é varrida em um período de tempo fixo. A seta verde é a velocidade. A seta roxa apontada para o Sol é a aceleração. Os planetas se movem em elipses ao redor do Sol (primeira lei de Kepler), varrem áreas iguais em tempos iguais (sua segunda lei) e têm períodos proporcionais ao seu semi-eixo maior elevado à potência de 3/2 (sua 3ª lei). Essas leis se aplicam igualmente bem a qualquer sistema solar gravitacional.

Ele pegou seu modelo bonito, elegante e atraente que discordava das observações e o jogou fora. Em vez disso, ele mergulhou nos dados para descobrir quais tipos de órbitas combinariam com o modo como os planetas realmente se moviam e chegou a um conjunto de conclusões científicas (não matemáticas).

1. Os planetas não se moviam em círculos ao redor do Sol localizado centralmente, mas sim em elipses com o Sol em um foco, com um conjunto diferente de parâmetros descrevendo a elipse de cada planeta.
2. Os planetas não se moviam a uma velocidade constante, mas sim a uma velocidade que variava com a distância do planeta ao Sol, de forma que os planetas varriam áreas iguais em tempos iguais.
3. E, finalmente, os planetas exibiam períodos orbitais que eram diretamente proporcionais ao longo eixo (o eixo maior) da elipse de cada planeta, elevado a uma potência específica (determinada como 3/2).

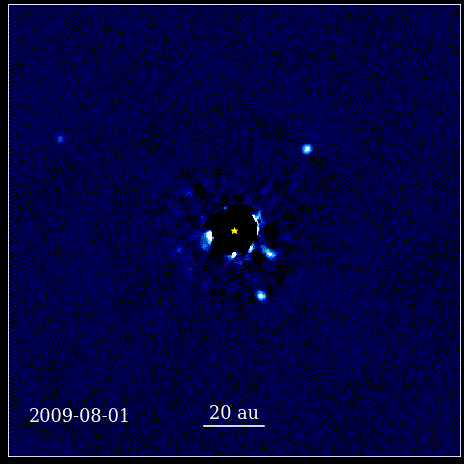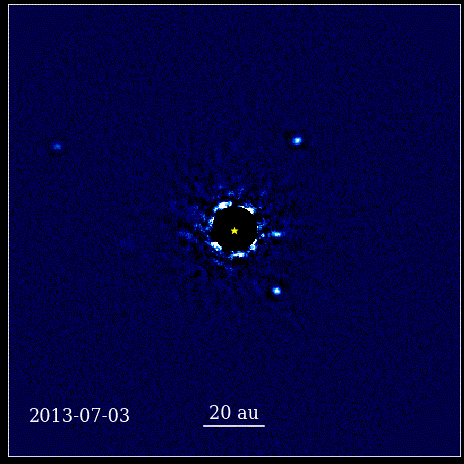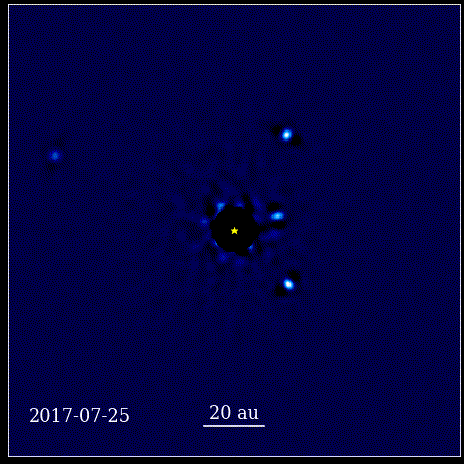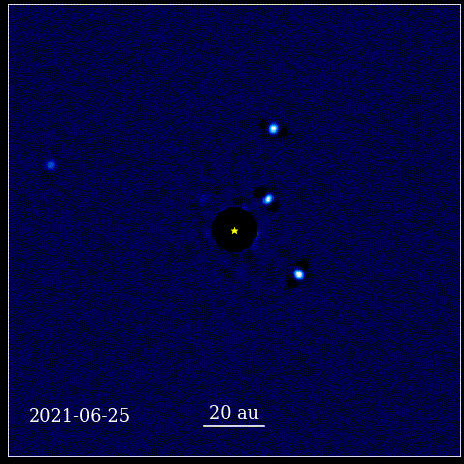Esta animação mostra os quatro planetas super-Júpiter fotografados diretamente em órbita ao redor da estrela, cuja luz é bloqueada por um coronógrafo, conhecido como HR 8799. Os quatro exoplanetas mostrados aqui estão entre os mais fáceis de obter imagens diretas devido ao seu grande tamanho e brilho, bem como sua enorme separação de sua estrela-mãe. Esses planetas que orbitam sua estrela obedecem às mesmas leis Keplerianas que os planetas do nosso próprio Sistema Solar.

Este foi um momento revolucionário na história da ciência. A matemática não estava na raiz das leis físicas que regem a natureza; era uma ferramenta que descrevia como as leis físicas da natureza se manifestavam. O principal avanço que aconteceu é que a ciência precisava se basear em observáveis ​​e mensuráveis, e que qualquer teoria precisava se confrontar com essas noções. Sem ela, o progresso seria impossível.

Essa ideia surgiu repetidas vezes ao longo da história, à medida que novas invenções e descobertas matemáticas nos capacitaram com novas ferramentas para tentar descrever sistemas físicos. Mas a cada vez, não era simplesmente que a nova matemática nos dizia como o Universo funcionava. Em vez disso, novas observações nos disseram que era necessário algo além de nossa física atualmente compreendida, e a matemática pura por si só era insuficiente para nos levar até lá.

Frequentemente visualizamos o espaço como uma grade 3D, mesmo que essa seja uma simplificação dependente do quadro quando consideramos o conceito de espaço-tempo. Na realidade, o espaço-tempo é curvado pela presença de matéria e energia, e as distâncias não são fixas, mas podem evoluir à medida que o Universo se expande ou se contrai. Antes de Einstein, o espaço e o tempo eram considerados fixos e absolutos para todos; hoje sabemos que isso não pode ser verdade.

No início dos anos 1900, ficou claro que a mecânica newtoniana estava com problemas. Não conseguia explicar como os objetos se moviam perto da velocidade da luz, levando à teoria especial da relatividade de Einstein. A teoria da gravitação universal de Newton também estava em apuros, pois não conseguia explicar o movimento de Mercúrio ao redor do Sol. Conceitos como espaço-tempo estavam apenas sendo formulados, mas a ideia de geometria não euclidiana (onde o próprio espaço poderia ser curvo, em vez de plano como uma grade 3D) estava flutuando há décadas entre os matemáticos.

Infelizmente, desenvolver uma estrutura matemática para descrever o espaço-tempo (e a gravitação) exigia mais do que matemática pura, mas a aplicação da matemática de uma maneira particular e ajustada que concordaria com as observações do Universo. É a razão pela qual todos conhecemos o nome “Albert Einstein”, mas muito poucas pessoas conhecem o nome “David Hilbert”.

Em vez de uma grade tridimensional vazia e em branco, colocar uma massa para baixo faz com que o que seriam linhas 'retas' se tornem curvas em um valor específico. A curvatura do espaço devido aos efeitos gravitacionais da Terra é uma visualização da energia potencial gravitacional, que pode ser enorme para sistemas tão maciços e compactos como o nosso planeta.

Ambos os homens tinham teorias que ligava a curvatura do espaço-tempo à gravidade e à presença de matéria e energia . Ambos tinham formalismos matemáticos semelhantes; hoje uma equação importante na Relatividade Geral é conhecida como a ação de Einstein-Hilbert. Mas Hilbert, que criou sua própria teoria independente da gravidade de Einstein, perseguia ambições maiores do que Einstein: sua teoria aplicada tanto à matéria quanto ao eletromagnetismo, bem como à gravidade.

E isso simplesmente não combinava com a natureza. Hilbert estava construindo uma teoria matemática que achava que deveria ser aplicada à natureza e nunca conseguiu obter equações bem-sucedidas que previssem os efeitos quantitativos da gravidade. Einstein o fez, e é por isso que as equações de campo são conhecidas como equações de campo de Einstein, sem mencionar Hilbert. Sem um confronto com a realidade, não temos física alguma.

Os elétrons exibem propriedades de onda, bem como propriedades de partículas, e podem ser usados ​​para construir imagens ou sondar tamanhos de partículas tão bem quanto a luz. Aqui, você pode ver os resultados de um experimento em que os elétrons são disparados um de cada vez através de uma fenda dupla. Uma vez que elétrons suficientes são disparados, o padrão de interferência pode ser visto claramente.

Essa situação quase idêntica ressurgiu poucos anos depois no contexto da física quântica. Você não poderia simplesmente disparar um elétron através de uma fenda dupla e saber, com base em todas as condições iniciais, onde ele terminaria. Um novo tipo de matemática — baseado na mecânica ondulatória e em um conjunto de resultados probabilísticos — era necessário. Hoje, usamos a matemática de espaços vetoriais e operadores, e os estudantes de física ouvem um termo que pode soar familiar: espaço de Hilbert .

Viaje pelo Universo com o astrofísico Ethan Siegel. Os assinantes receberão a newsletter todos os sábados. Todos a bordo!

O mesmo matemático, David Hilbert, descobriu um conjunto de espaços vetoriais matemáticos que era extremamente promissor para a física quântica. Só que, mais uma vez, suas previsões não faziam muito sentido quando confrontadas com a realidade física. Para isso, alguns ajustes precisaram ser feitos na matemática, criando o que alguns chamam um espaço de Hilbert manipulado ou um espaço físico de Hilbert. (Onde o “produto interno” daquele espaço de Hilbert tinha restrições físicas impostas a ele, mas não por qualquer motivo matematicamente motivado.) As regras matemáticas precisavam ser aplicadas com certas ressalvas específicas, ou os resultados de nosso universo físico nunca seriam recuperáveis .

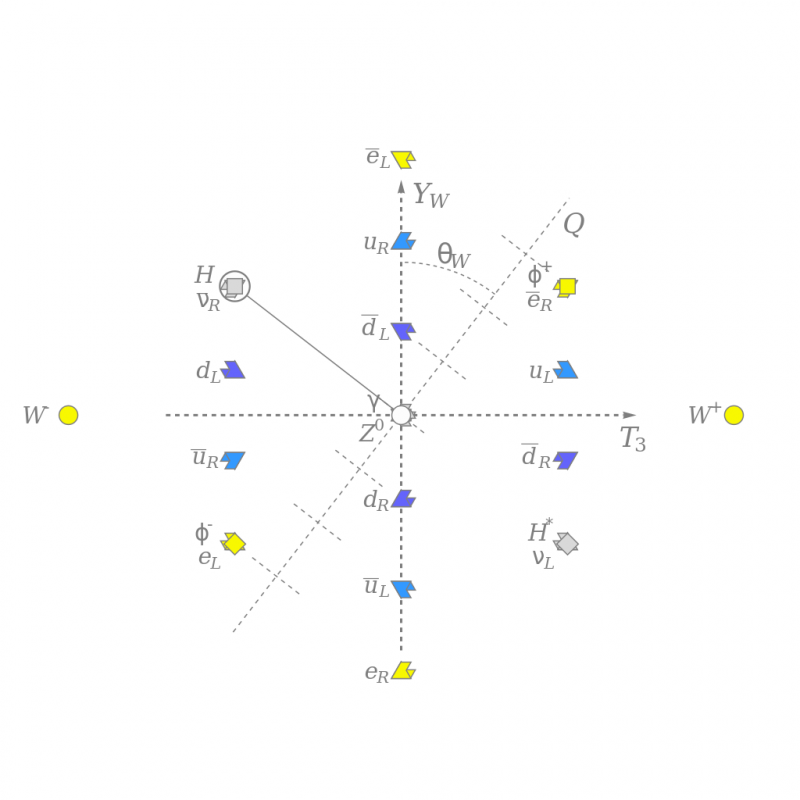O padrão de isospin fraco, T3, e hipercarga fraca, Y_W, e carga de cor de todas as partículas elementares conhecidas, giradas pelo ângulo de mistura fraco para mostrar a carga elétrica, Q, aproximadamente ao longo da vertical. O campo neutro de Higgs (quadrado cinza) quebra a simetria eletrofraca e interage com outras partículas para dar-lhes massa. Este diagrama mostra a estrutura das partículas, mas está enraizado tanto na matemática quanto na física.

Hoje, está muito na moda na física teórica apelar para a matemática como um caminho potencial para uma teoria ainda mais fundamental da realidade. Várias abordagens baseadas em matemática foram tentadas ao longo dos anos:

• impondo simetrias adicionais,
• adicionando dimensões extras,
• adicionando novos campos na Relatividade Geral,
• adicionando novos campos à teoria quântica,
• usando grupos maiores (da teoria matemática dos grupos) para estender o Modelo Padrão,

juntamente com muitos outros. Essas explorações matemáticas são interessantes e potencialmente relevantes para a física: elas podem conter pistas sobre quais segredos o Universo pode ter guardado além do que é conhecido atualmente. Mas a matemática sozinha não pode nos ensinar como o Universo funciona. Não obteremos respostas definitivas sem confrontar suas previsões com o próprio Universo físico.

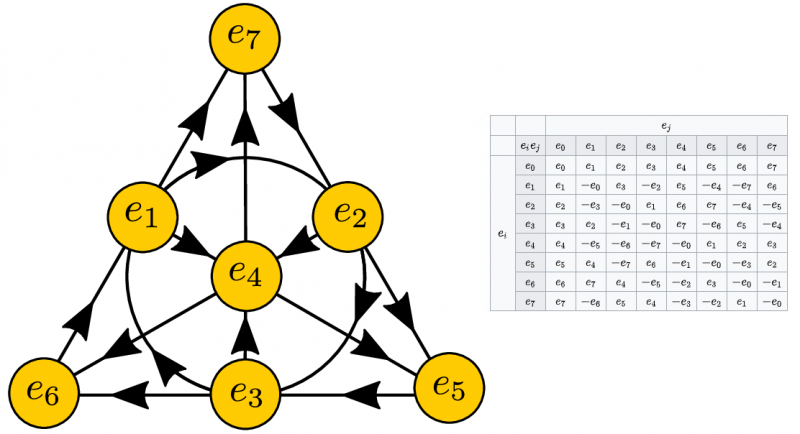Visualizar a multiplicação da unidade octônios, dos quais existem 8, requer pensar em espaços de dimensões superiores (esquerda). A tabuada de multiplicação para quaisquer octônios de duas unidades também é mostrada (à direita). Octônios são uma estrutura matemática fascinante, mas oferecem soluções não únicas para uma miríade de possíveis aplicações físicas.

De certa forma, é uma lição que todo estudante de física aprende na primeira vez que calcula a trajetória de um objeto lançado ao ar. Até onde isso vai? Onde ele pousa? Quanto tempo fica no ar? Quando você resolve as equações matemáticas — as equações de movimento de Newton — que governam esses objetos, você não obtém 'a resposta'. Você obtém duas respostas; é isso que a matemática te dá.

Mas, na realidade, há apenas um objeto. Ele segue apenas uma trajetória, pousando em um local em um horário específico. Qual resposta corresponde à realidade? A matemática não vai te dizer. Para isso, você precisa entender as particularidades do problema de física em questão, pois somente isso lhe dirá qual resposta tem um significado físico por trás dela. A matemática o levará muito longe neste mundo, mas não o levará a tudo. Sem um confronto com a realidade, você não pode esperar entender o universo físico.

Compartilhar: